Question

A man running on a horizontal road at $8km{{h}^{-1}}$ finds the rain falling vertically. He increases his speed to $12km{{h}^{-1}}$ and finds that the drops make angle ${{30}^{\circ }}$with the vertical. Find the speed and direction of the rain with respect to the road.

Answer 1

Hint: For rain-man problems like these, we must first find the velocity of rain with respect to man by finding the x-component and y-component of velocity separately. The velocity must have two components because it makes a certain angle with vertical. Then, we shall apply the basic formulae of vectors to find magnitude and direction of velocity of rain with respect to road.

Complete answer:
The relative velocity between rain and the man is given as:
${{V}_{RM}}={{V}_{RG}}-{{V}_{MG}}$ …………….. equation (1)
Where,
${{V}_{RM}}=$ velocity of rain with respect to man
${{V}_{RG}}=$ velocity of rain with respect to ground
${{V}_{MG}}=$ velocity of man with respect to ground
Let velocity of rain with respect to road be ${{V}_{RG}}={{\left( {{V}_{RG}} \right)}_{x}}\hat{i}+{{\left( {{V}_{RG}} \right)}_{y}}\hat{j}$
Now, in the x-direction (or the horizontal direction);

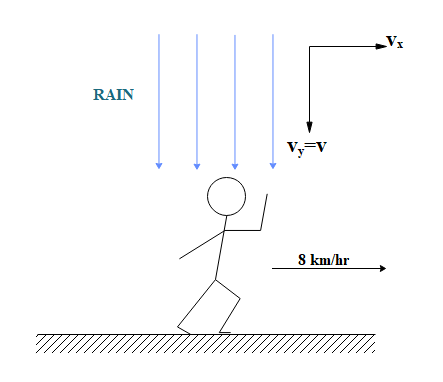
When rain appears to be falling vertically on man, velocity of man with respect to ground is $8km{{h}^{-1}}$ in the positive x-direction.
$\Rightarrow {{\left( {{V}_{MG}} \right)}_{x}}=8km{{h}^{-1}}$
 Therefore, the velocity of rain with respect to man in the horizontal direction (x-direction) is zero.
$\Rightarrow {{\left( {{V}_{RM}} \right)}_{x}}=0$
Applying equation (1) for relative motion in x-direction:
${{\left( {{V}_{RM}} \right)}_{x}}={{\left( {{V}_{RG}} \right)}_{x}}-{{\left( {{V}_{MG}} \right)}_{x}}$
$\Rightarrow 0={{\left( {{V}_{RG}} \right)}_{x}}-8$
$\Rightarrow {{\left( {{V}_{RG}} \right)}_{x}}=8km{{h}^{-1}}$ ……………… equation (2)
Therefore, the horizontal component of velocity of rain is $8km{{h}^{-1}}$.
As the man increases his velocity to $12km{{h}^{-1}}$, the rain drops seem to be making an angle of ${{30}^{\circ }}$ with the vertical.

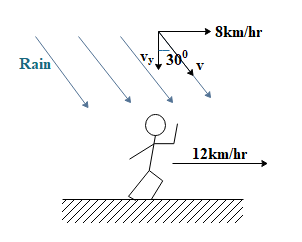
We shall first look in the x-direction.
In this case ${{\left( {{V}_{RM}} \right)}_{x}}\ne 0$ and ${{\left( {{V}_{MG}} \right)}_{x}}=12km{{h}^{-1}}$, therefore the velocity of rain with respect to ground in this case is:
From equation (1), ${{\left( {{V}_{RM}} \right)}_{x}}={{\left( {{V}_{RG}} \right)}_{x}}-{{\left( {{V}_{MG}} \right)}_{x}}$ and from equation (2), ${{\left( {{V}_{RG}} \right)}_{x}}=8km{{h}^{-1}}$,
$\begin{align}
  & \Rightarrow {{\left( {{V}_{RM}} \right)}_{x}}=8-12 \\
 & \Rightarrow {{\left( {{V}_{RM}} \right)}_{x}}=-4km{{h}^{-1}} \\
\end{align}$
 From the general equation of vectors, we know that for vector having components in x and y-direction respectively, $\tan \theta =\dfrac{{{v}_{x}}}{{{v}_{y}}}$
Where, $\theta =$angle made by the vector with the given reference point
Using this, we find
$\tan {{30}^{\circ }}=\dfrac{{{\left( {{V}_{RM}} \right)}_{x}}}{{{\left( {{V}_{RM}} \right)}_{y}}}$
$\begin{align}
  & \Rightarrow \dfrac{1}{\sqrt{3}}=\dfrac{4}{{{\left( {{V}_{RM}} \right)}_{y}}} \\
 & \Rightarrow {{\left( {{V}_{RM}} \right)}_{y}}=4\sqrt{3}km{{h}^{-1}} \\
\end{align}$
In the y-direction:
${{\left( {{V}_{RM}} \right)}_{y}}={{\left( {{V}_{RG}} \right)}_{y}}-{{\left( {{V}_{MG}} \right)}_{y}}$
But since the velocity of man with respect to ground is zero in vertical direction \[\left\{ {{\left( {{V}_{MG}} \right)}_{y}} \right\}\] , we get
$\begin{align}
  & \Rightarrow 4\sqrt{3}={{\left( {{V}_{RG}} \right)}_{y}}-0 \\
 & \Rightarrow {{\left( {{V}_{RG}} \right)}_{y}}=4\sqrt{3}km{{h}^{-1}} \\
\end{align}$
Therefore, the magnitude of velocity of rain with respect to road is:
${{V}_{RG}}=\sqrt{\left( {{V}_{RG}} \right)_{x}^{2}+\left( {{V}_{RG}} \right)_{y}^{2}}$
$\begin{align}
  & \Rightarrow {{V}_{RG}}=\sqrt{{{\left( 8 \right)}^{2}}+{{\left( 4\sqrt{3} \right)}^{2}}} \\
 & \Rightarrow {{V}_{RG}}=\sqrt{64+48} \\
 & \Rightarrow {{V}_{RG}}=\sqrt{112}km{{h}^{-1}} \\
\end{align}$
$\therefore {{V}_{RG}}=10.58km{{h}^{-1}}$
Again using $\tan \theta =\dfrac{{{v}_{x}}}{{{v}_{y}}}$for velocity of rain with respect to ground:
$\begin{align}
  & \Rightarrow \tan \theta =\dfrac{8}{4\sqrt{3}} \\
 & \Rightarrow \tan \theta =\dfrac{2}{\sqrt{3}} \\
\end{align}$
$\begin{align}
  & \therefore \theta ={{\tan }^{-1}}\left( \dfrac{2}{\sqrt{3}} \right) \\
 & \therefore \theta \approx {{41}^{\circ }} \\
\end{align}$
Therefore, the magnitude of velocity of rain with respect road is $10.58km{{h}^{-1}}$ and it makes an angle of ${{\tan }^{-1}}\left( \dfrac{2}{\sqrt{3}} \right)$ (which is approximately ${{41}^{\circ }}$) with the vertical.

Note:
As the man increases his speed, the angle made by velocity of rain with respect to man also increases. In this scenario, if the man is holding an umbrella, he will get more wet and the umbrella would not be able to prevent rain as the man starts running faster.