Question

A man on the top of a bamboo pole observes that the angle of depression of the base and the top of another pole is $60{}^\circ \text{ and 30}{}^\circ $ , respectively. If the second pole stands 5m above the ground level, then the height of the bamboo, on which the man is sitting is:
(a) 5m
(b) 7.5m
(c) 10m
(d) 12.5m

Answer 1

Hint: First draw a rough diagram of the given conditions. Now, assume that the height of the bamboo pole is ‘h’ and its distance from the tower is ‘d’. Form two equations in ‘h’ and ‘d’ using the information provided and solve these two equations to get the value of ‘h’ and ‘d’. Use $\tan \theta =\dfrac{\text{perpendicular}}{\text{base}}$ to form the equations in the right angle triangle.

Complete step-by-step answer:
Let us assume that P is the bottom of the pole and Q is the top of the pole. It is taken that the top of the bamboo pole is denoted by B and bottom as A. So, let us draw the diagram of the given situation.

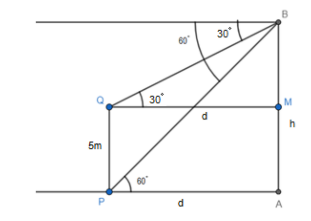
From the above figure, we have,
In right angle triangle PAB,
AP = d, AB = h
\[\angle APB=60{}^\circ \] , as from the figure we can see that angle of depression of the bottom of the pole are alternate interior angles, and alternate interior angles are equal.
Therefore, using $\tan \theta =\dfrac{\text{perpendicular}}{\text{base}}$, we have,
$\begin{align}
  & \tan 60{}^\circ =\dfrac{AB}{AP} \\
 & \Rightarrow \tan 60{}^\circ =\dfrac{h}{d} \\
 & \Rightarrow d=\dfrac{h}{\tan 60{}^\circ }........................(i) \\
\end{align}$
Now, in right angle triangle BQM,
QM = AP = d, as they are the opposite sides of the rectangle PAMQ.
BM = AB – AM = h-5 , because it is given that the height of the pole is 5m and here we have assumed the pole as PQ and PQ is equal to AM.
Also, \[\angle BQM=30{}^\circ \] , as from the figure we can see that angle of depression of the top of the pole are alternate interior angles, and alternate interior angles are equal.
Therefore, using $\tan \theta =\dfrac{\text{perpendicular}}{\text{base}}$, we have,
$\begin{align}
  & \tan 30{}^\circ =\dfrac{BM}{QM} \\
 & \Rightarrow \tan 30{}^\circ =\dfrac{h-5}{d} \\
 & \Rightarrow h-5=d\tan 30{}^\circ \\
 & \Rightarrow \dfrac{h-5}{\tan 30{}^\circ }=d.........................(ii) \\
\end{align}$
Now if we put the value of d from equation (i), we get
$\dfrac{h-5}{\tan 30{}^\circ }=\dfrac{h}{\tan 60{}^\circ }$
We know that $\tan 30{}^\circ =\dfrac{1}{\sqrt{3}}\text{ and tan60}{}^\circ \text{=}\sqrt{3}$ .
$\left( h-5 \right)\sqrt{3}=\dfrac{h}{\sqrt{3}}$
$\Rightarrow 3h-15=h$
$\Rightarrow 2h=15$
$\Rightarrow h=7.5m$
Therefore, the height of the bamboo pole is $7.5\text{ meters}$ . So, the answer to the above question is option (b).

Note: We must substitute and eliminate the variables properly otherwise we may get confused while solving the equations. Here, in the above question we have used a tangent of the given angle because we have to find both, height of the tower and its distance from the post. So, the function relating these two variables is tangent of the angle.