Question

A man on the deck of a ship is 10 m above the water level. He observes that the angle of elevation of the top of the cliff is ${{45}^{\circ }}$ and the angle of a depression of the base is ${{30}^{\circ }}$ . Calculate the distance of the cliff from the ship and the height of the cliff.

Answer 1

Hint: We first draw the figure according to the information given in the question. Assume the distance of the cliff from the ship be ‘x’ and height of the cliff be $\left( 10+h \right)$ meters. Consider a triangle, use$\text{tan }\!\!\theta\!\!\text{ =}\dfrac{\text{perpendicular}}{\text{base}}$ in that triangle to find the relation between x and h. Now, consider another triangle and use $\tan \theta =\dfrac{p}{b}$ in that triangle to find the value x. After that calculate h using the relation between h and x obtained above. Now the height of the cliff would be $\left( 10+h \right)$ m.

Complete step by step answer:

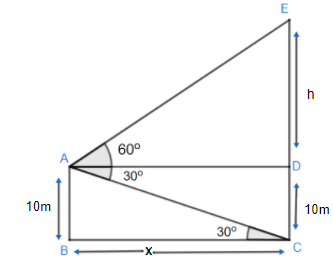
Let a man stand on the deck of a ship at point A, such that AB$=10m$ and let CE be the hill.
Thus, $AB=CD=10m$
The top and bottom of a hill E and C respectively.
Given, we have the angle of depression of the base C of the hill observed from A in ${{30}^{\circ }}$ and the angle of elevation of the top of the hill observed from A is ${{60}^{\circ }}$ .
Then, we can clearly see in the figure
$\angle EAD={{60}^{\circ }}$ and
$\angle CAD=\angle BCA={{30}^{\circ }}$ (Alternate angles)
Let, we have,
$AD=BC=x$ meters
And $DE=h$ meters.
Now, we consider $\Delta ADE$ ,
So, in $\Delta ADE$ , $\text{tan}\angle \text{EAD=}\dfrac{\text{perpendicular}}{\text{base}}$ .
$\tan \angle EAD=\dfrac{DE}{AD}$
We have, $\angle EAD={{60}^{\circ }}$ .
$DE=h$ meters
$AD=x$ meters.
$\Rightarrow \tan {{60}^{\circ }}=\dfrac{h}{x}$ , ( we know that, $\tan {{60}^{\circ }}=\sqrt{3}$ )
$\Rightarrow \sqrt{3}=\dfrac{h}{x}$ ,
$\Rightarrow h=\sqrt{3}x$ ……………………. (1)
Now, we consider $\Delta ABC$ ,
So, in $\Delta ABC$ we have $\tan \angle DAC=\dfrac{AB}{BC}$ .
As, $\text{tan }\!\!\theta\!\!\text{ =}\dfrac{\text{perpendicular}}{\text{base}}$ and we know, $\angle DAC={{30}^{\circ }}$
$\therefore \tan {{30}^{\circ }}=\dfrac{AB}{BC}$ , we have,
$AB=10$ meters, $BC=x$ meters.
$\Rightarrow \dfrac{1}{\sqrt{3}}=\dfrac{10}{x}$ (Since, we know that $\tan {{30}^{\circ }}=\dfrac{1}{\sqrt{3}}$ )
$\Rightarrow x=10\sqrt{3}$ Meters…………………….. (2)
Now, we can substitute the value of x from equation (2) in equation (1), we have
\[\begin{align}
  & \Rightarrow h=\sqrt{3}x \\
 & \Rightarrow h=\left( \sqrt{3}\times 10\sqrt{3} \right) \\
 & \Rightarrow h=\left( 10\times 3 \right) \\
 & \Rightarrow h=30 \\
\end{align}\]

So, the height of the hill is 40 m & the distance of the hill from the ship is $10\sqrt{3}$ meter.

Note: Students generally make mistakes in recognizing the angle of depression.

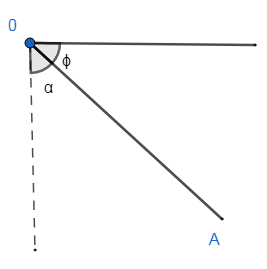
If from point ‘O’, we are watching point ‘A’, angle ‘∅’ is the angle of depression. But students get confused and take angle ‘α’ as an angle of depression.