Question

A man of mass $M$ stands on a weighing machine in an elevator accelerating upwards with an acceleration $a$. Draw the free-body diagram of the man as observed by the observer A (stationary on the ground and observer B (stationary on the elevator). Also, calculate the reading of the weighing machine.

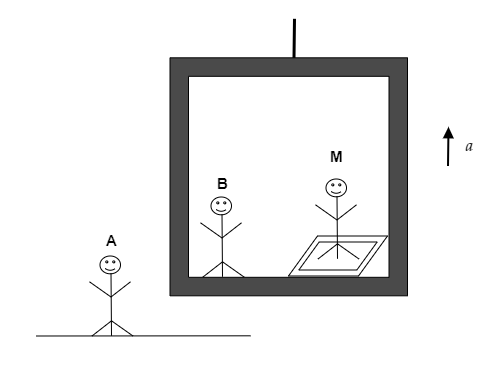
Answer 1

Hint:The free-body diagram represents the direction of the forces in play for a system. The observer A standing on the ground will notice the elevator or the man being accelerated but the observer B inside the elevator will not observe this acceleration. Also for observer B, a pseudo force will exist in the downward direction along with the weight of the man M as the man exists in a non-inertial frame of reference when observed by observer B.

Complete step by step answer.
Step 1: Sketch the free body diagram of the man M as seen by observer A.
To the observer A, the forces acting on the man in the elevator are his weight $W = mg$ directed downwards and the normal force $N$ acting upwards.
The free-body diagram as viewed by observer A is given below.

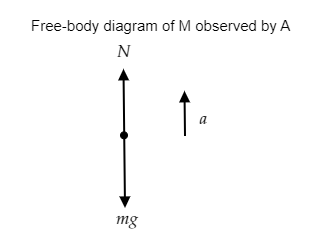
Now we can express the force equation to determine the reading on the weighing machine observed by observer A.
We have $N - mg = ma$ --------- (1)
$ \Rightarrow N = m\left( {g + a} \right)$
The normal force $N$ represents the reading on the weighing machine.
Thus the reading on the weighing scale will be $N = m\left( {g + a} \right)$ .
Step 2: Sketch the free body diagram of the man M as seen by observer B.
To the observer B, the forces acting on the man in the elevator are his weight $W = mg$ directed downward and the normal force $N$ acting upward. In addition to these forces, a pseudo force ${F_{pseudo}} = ma$ is also directed downwards.
The free-body diagram as viewed by observer B is given below.

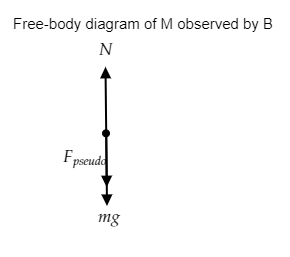
Now we can express the force equation to determine the reading on the weighing machine observed by observer B. Observer B does not feel the acceleration of the elevator.
So we have $N - mg - ma = 0$ --------- (2)
$ \Rightarrow N = m\left( {g + a} \right)$
Thus the reading of the weighing scale will be $N = m\left( {g + a} \right)$ .
So the reading on the weighing machine is the same in both cases.

Note:The force term $F = ma$ in equation (1) is due to the acceleration of the elevator directed upwards while the term ${F_{pseudo}} = ma$ in equation (2) is due to the pseudo force directed downwards. To observer B, the man is at rest in the elevator and so L.H.S of equation (2) is zero. Pseudo force is an imaginary force that describes the motion of an object in a non-inertial frame of reference. A non-inertial frame of reference is an accelerated frame of reference (accelerated elevator).