Question

A man of mass M stands at one end of a stationary plank of length L, lying on a smooth surface. The man walks to the other end of the plank. If the mass of the plank is M/3, the distance that the man moves relative to the ground is.

(A). 3L/4
(B). L/4
(C). 4L/5
(D). L/3

Answer 1

Hint: Draw the diagram as it is described in the question, then as we know that the total length of plank is L so we can create an equation of the length of log. Then figure out the equation of center of mass in terms of the values of the plank, create another equation from this formula and compare those to get the distance the man moves.

Complete step-by-step answer:

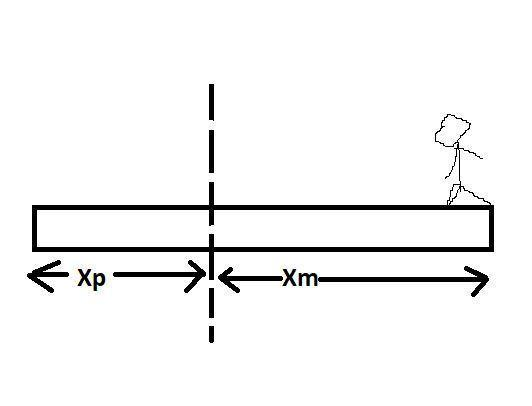
In the diagram is a man who moved from the dotted line to the right end of the plank,
We can say that ,
${{X}_{p}}+{{X}_{m}}=L$ …… Eq.1
As the surface is smooth, hence no force is required for movement along x axis,
Now , we can say that along x-axis center of mass is stationary,
And we know that the movement of center of mass is:
${{X}_{cm}}=\dfrac{M({{X}_{m}})+\dfrac{M}{3}(-{{X}_{p}})}{\dfrac{4m}{3}}$ ,
Here M is the mass of the man, ${{X}_{m}}$ is the displacement of the man,
M/3 is the mass of plank, and ${{X}_{p}}$ is the displacement, and 4m/3 is the mass of the whole system.
As there is no velocity, as no external force is applied hence, ${{X}_{cm}}$=0.
Therefore,
$0=({{X}_{m}})+\dfrac{1}{3}(-{{X}_{p}})$
On solving this we get ,
${{X}_{p}}=3{{X}_{m}}$……. Eq.2
Now on comparing Eq.1 and Eq.2 ,
We get,
${{X}_{m}}=\dfrac{L}{4}$ .
Therefore option D is the correct option.

Note: As the plank is considered frictionless hence there is no friction and the body over it can move without applying any force hence as no external force is applied we are considering the velocity as null.