Question

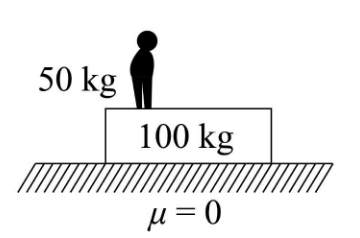
A man of mass \[50{\rm{ kg}}\] is standing on a \[100{\rm{ kg}}\] plank kept on a frictionless horizontal floor. Initially both are at rest. If the man starts walking on the plank with speed \[6{\rm{ }}{{\rm{m}} {\left/{\vphantom {{\rm{m}} {\rm{s}}}} \right.} {\rm{s}}}\] towards right relative to the plank, then amount of muscle energy spent by the man is

(1) \[600{\rm{ J}}\]
(2) \[200{\rm{ J}}\]
(3) \[400{\rm{ J}}\]
(4) \[500{\rm{ J}}\]

Answer 1

Hint:We will use the law of conservation of momentum for the given man and plank system. As there is no external force applying on the system; therefore, muscle energy spent by the man will be converted into the total kinetic energy of the system.

Complete step by step answer:
Given:
The mass of the man is \[{m_1} = 50{\rm{ kg}}\].
The mass of the plank is \[{m_2} = 100{\rm{ kg}}\].
The speed with which man starts moving is \[{V_1} = 6{\rm{ }}{{\rm{m}} {\left/
 {\vphantom {{\rm{m}} {\rm{s}}}} \right.
 } {\rm{s}}}\].
The coefficient of friction between plank and ground is \[\mu = 0\].
We can see that there is no external force applied to the man and plank system. It is also given that the coefficient of friction between plank and ground is zero, that means the surface is frictionless.
When the man starts moving on the plank in the right direction, due to the absence of friction between plank and surface plank will start moving in the opposite direction with a velocity which can be denoted by \[{V_2}\].
Let us consider plank as an observing frame so the expression for conservation of momentum for the man and plank system can be written as:
\[{m_1}\left( {{V_1} - {V_2}} \right) = {m_2}{V_2}\]
Here \[\left( {{V_1} - {V_2}} \right)\] is the relative velocity of the man with respect to the plank.
We will substitute \[50{\rm{ kg}}\] for \[{m_1}\], \[100{\rm{ kg}}\] for \[{m_2}\] and \[6{\rm{ }}{{\rm{m}} {\left/
 {\vphantom {{\rm{m}} {\rm{s}}}} \right.
 } {\rm{s}}}\] for \[{V_1}\] in the above expression to the velocity of the plank.
\[
\Rightarrow\left( {50{\rm{ kg}}} \right)\left( {6{\rm{ }}{{\rm{m}} {\left/
 {\vphantom {{\rm{m}} {\rm{s}}}} \right.
 } {\rm{s}}} - {V_2}} \right) = \left( {100{\rm{ kg}}} \right){V_2}\\
\Rightarrow{V_2} = 2{\rm{ }}{{\rm{m}} {\left/
 {\vphantom {{\rm{m}} {\rm{s}}}} \right.
 } {\rm{s}}}
\]
We can write the total kinetic energy of the system as the summation of the kinetic energy of man and kinetic energy of plank.
\[K.E. = \dfrac{1}{2}{m_1}{\left( {{V_1} - {V_2}} \right)^2} + \dfrac{1}{2}{m_2}V_2^2\]
We will substitute \[50{\rm{ kg}}\] for \[{m_1}\], \[100{\rm{ kg}}\] for \[{m_2}\], \[6{\rm{ }}{{\rm{m}} {\left/
 {\vphantom {{\rm{m}} {\rm{s}}}} \right.
 } {\rm{s}}}\] for \[{V_1}\] and \[6{\rm{ }}{{\rm{m}} {\left/
 {\vphantom {{\rm{m}} {\rm{s}}}} \right.
 } {\rm{s}}}\] for \[{V_2}\] in the above expression to get the value of total kinetic energy.
\[
K.E. = \dfrac{1}{2}\left( {50{\rm{ kg}}} \right){\left( {6{\rm{ }}{{\rm{m}} {\left/
 {\vphantom {{\rm{m}} {\rm{s}}}} \right.
 } {\rm{s}}} - 2{\rm{ }}{{\rm{m}} {\left/
 {\vphantom {{\rm{m}} {\rm{s}}}} \right.
 } {\rm{s}}}} \right)^2} + \dfrac{1}{2}\left( {100{\rm{ kg}}} \right){\left( {2{\rm{ }}{{\rm{m}} {\left/
 {\vphantom {{\rm{m}} {\rm{s}}}} \right.
 } {\rm{s}}}} \right)^2}\\
\Rightarrow K.E.= 600{\rm{ kg}} \cdot {{{{\rm{m}}^2}} {\left/
 {\vphantom {{{{\rm{m}}^2}} {{{\rm{s}}^2}}}} \right.
 } {{{\rm{s}}^2}}} \times \left( {\dfrac{{\rm{N}}}{{{\rm{kg}} \cdot {{\rm{m}} {\left/
 {\vphantom {{\rm{m}} {{{\rm{s}}^2}}}} \right.
 } {{{\rm{s}}^2}}}}}} \right)\\
\Rightarrow K.E. = 600{\rm{ Nm}} \times \left( {\dfrac{{\rm{J}}}{{{\rm{Nm}}}}} \right)\\
\therefore K.E. = 600{\rm{ J}}
\]
The value of the total kinetic energy of the man and plank system is equal to the muscle energy of the system. Therefore, muscle energy spent by the man is \[600{\rm{ J}}\], and option (1) is correct.

Note:While writing the equation of momentum conservation does not forget to consider the relative velocity of man. We can remember the conversion of unit Newton into its base units (kg, m, s). We can also note that Newton-metre gives the unit of energy that is Joule.