Question

A man of mass $50kg$ stands on a frame of mass $30kg$. He pulls on a light rope which passes over a pulley. The other end of the rope is attached to the frame. For the system to be in equilibrium, what force man must exert on the rope?

Answer 1

Hint:Here, a man is pulling a rope in downward direction, therefore, tension is created in both the sides of the rope acting in upward direction. The weight of a man and frame both act in downward direction. Thus, for the system to be in the equilibrium, these both upward and downward forces should be balanced.

Formula used:
$W = mg$,
Where $W$ is the weight of the body, $m$ is the mass of the body and $g$ is the gravitational acceleration

Complete step by step answer:
Let us understand the forces acting in this case as by the help of a diagram. Here, The force exerted by the man is equal to the tension developed in the rope.

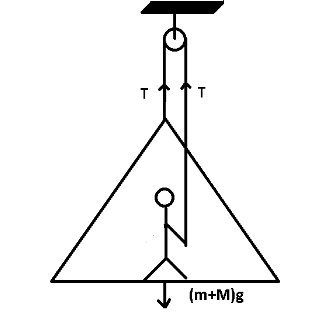
Here, the tensile \[W = \left( {m + M} \right)g = \left( {80g} \right)N\] force is balanced by the downward force due to the weight of the man and the frame. The mass of the frame $m = 30kg$ and the mass of the man $M = 50kg$. Now the man is standing on a frame. Therefore, the total mass of the system is $m + M = 30 + 50 = 80kg$

As shown in figure, total downward force on the system is the weight of the system \[W = \left( {m + M} \right)g = \left( {80g} \right)N\]
And total upward force will be $T + T = \left( {2T} \right)N$
For the equilibrium condition,
$
2T = W \\
\Rightarrow 2T = 80g \\
\therefore T = 40g \\ $
We know that this tension is equal to the force with which the man is pulling the rope. Thus, we can say that the man must exert a force of $40g$ for the system to be in equilibrium.

Hence, option (A) is the right answer.

Note: Here, we have rope on both the sides of pulley with a downward force on each end. In this case, the system is in equilibrium. Because of this, we have considered that the tension on both the sides of the rope is equal. Tension can be defined as an action-reaction pair of forces acting at each end of the said elements. While considering a rope, the tension force is felt by every section of the rope in both the directions, apart from the endpoints. The endpoints experience tension on one side and the force from the weight attached.