Question

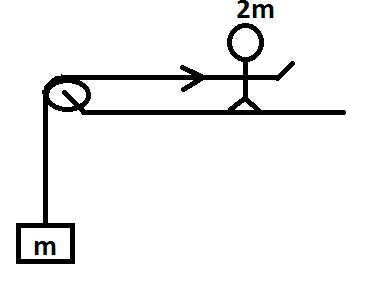
A man of mass \[\text{2m}\] is pulling up a block of mass \[\text{m}\] with constant velocity. The acceleration of man is- (Neglect any friction)-

(A). \[\text{g}\]
(B). \[\text{2g}\]
(C). \[\text{3g}\]
(D). \[{\text{g}}/{2}\;\]

Answer 1

Hint: The figure has two separate systems and different forces are acting on each system. Resolve the systems. There are two main forces- tension in string and weight of block. Analyse each system and make equations. Solve the equations to find acceleration of man.

Formula used:
 \[\Rightarrow \text{ T = mg}\]
 \[\text{mg = 2ma }\!\!'\!\!\text{ }\]

Complete step-by-step answer:
The block, pulley and man form an isolated system.

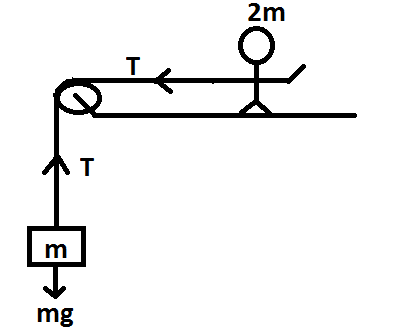
Let us divide the fig into two systems- the block and pulley system and the man and pulley system and consider the upward direction as \[(\text{+}\text{)}\] .
 Forces acting on block and pulley system are- \[\text{T}\] and \[\text{mg}\] , where \[\text{T}\] is the tension in the string and \[\text{mg}\] is the weight acting on the block. The block is moving with uniform velocity in the upward direction which means there are no external forces acting on block, so,
 \[\text{a= 0}\] Here \[\text{a}\] is acceleration of block
Therefore-
 \[\text{T - mg = 0}\]
 \[\Rightarrow \text{ T = mg}\] - (1)
Force acting on the man pulley system is \[\text{T}\] and the system is moving opposite the direction of \[\text{T}\] with some acceleration. Therefore,
 \[\text{T = (2m)a }\!\!'\!\!\text{ }\] - (2)
 \[\text{2m}\] is mass of man, \[\text{a }\!\!'\!\!\text{ }\] is acceleration of man.
From eq (1) and eq (2), we get,
 \[\begin{align}
  & \text{mg = 2ma }\!\!'\!\!\text{ } \\
 & \Rightarrow \text{ a }\!\!'\!\!\text{ = }\dfrac{g}{2} \\
\end{align}\]
Therefore the acceleration of man is \[\dfrac{\text{g}}{2}\] .

So, the correct answer is “Option D”.

Note: It is important to resolve the two systems because in the block- pulley system, there are no external forces hence their motion is uniform while in the man- pulley system, external forces are acting on man due to which it has non-uniform motion. The pulley is considered to be at rest.