Question

A man of height $1.8m$ is standing near a pyramid. If the shadow of the man is of length $2.7m$ and the shadow of the pyramid is $210m$ long at that instant, find the length of the pyramid.

Answer 1

Hint: A pair of triangle is called to be similar if their ratio of the perpendicular side to the base of one triangle is same as the ratio of the perpendicular side to the base of the other triangle but size of both the triangles may be different.

Complete step-by-step answer:
Let us first draw the figure according to the question:
Let AB be the height of the pyramid,
EC be the length of the shadow of the man and
BC be the length of the shadow of the pyramid.
So, we construct the diagram with the man as ED and the pyramid as AB:

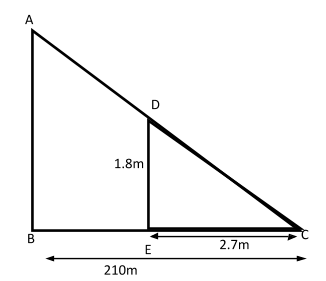
Now, we have $DE = 1.8m,BC = 210m$and$EC = 2.7m$.
Here the length of AB and length of AC of right$\Delta ABC$are proportional to the corresponding parts of the right $\Delta DEC$.
$\therefore \Delta ABC$ is similar to $\Delta DEC$.$\Delta ABC$
Hence, $\dfrac{{AB}}{{DE}} = \dfrac{{BC}}{{EC}}$
By substituting the values of DE, BC and EC we get,
\[\dfrac{{AB}}{{1.8m}} = \dfrac{{210m}}{{2.7m}}\]
By shifting the denominator of L.H.S to R.H.S, we get
$ \Rightarrow AB = \dfrac{{210m}}{{2.7m}} \times 1.8m$
On further solving the equation by converting it into its simplest form so that we get the value of AB.
We have,$AB = 140m$.

$\therefore $The length of the pyramid is $140m$.

Note: If all three angles of the triangle are congruent but the sides are not, then one of the triangles is a scaled up version of the other. When this happens the proportions between the sides still remains unchanged which is the criteria for similarity. Here we have, $\Delta ABC$ is similar to $\Delta DEC$.$\Delta ABC$
Hence, $\dfrac{{AB}}{{DE}} = \dfrac{{BC}}{{EC}}$.