Question

A man of height 170cm wants to see his complete image in a plane mirror (while standing). His eyes are at a height of 160 cm from the ground.
A. minimum length of the mirror = 80 cm
B. minimum length of the mirror = 85 cm
C. bottom of the mirror should be at a height 80 cm or more
D. bottom of the mirror should be at a height 85 cm

Answer 1

Hint: The easy method to solve this problem is to calculate the half the value of the height of a man to find the value of the minimum length of the mirror and to find the bottom position of the mirror, the half the value of the height of the eyes from the ground should be calculated.
Formula used:
\[{{L}_{\min }}=\dfrac{H}{2}\]

Complete step-by-step solution:
From given, we have the data,
The height of a man = 170 cm
The height of the eyes of a man from the ground = 160 cm
There are two methods to solve this problem.
The method I: Direct method
The minimum length of a plane mirror to see the full height of one’s body is,
\[{{L}_{\min }}=\dfrac{H}{2}\]
Where H is the height of the person.
The height of a man is = 170 cm
So, we get the minimum length of the mirror to be,
\[\begin{align}
  & {{L}_{\min }}=\dfrac{170}{2} \\
 & {{L}_{\min }}=85\,cm \\
\end{align}\]
Therefore, the minimum length of the mirror is 85 cm.
The eyes of a man are at a height from the ground = 160 cm
So, we get the position of the mirror to be,
\[\begin{align}
  & {{L}_{\min }}=\dfrac{160}{2} \\
 & {{L}_{\min }}=80\,cm \\
\end{align}\]
Therefore, the bottom of the mirror should be at a height of 80 cm or more.
Method II: Indirect method
The ray diagram of a plane mirror is as follows:

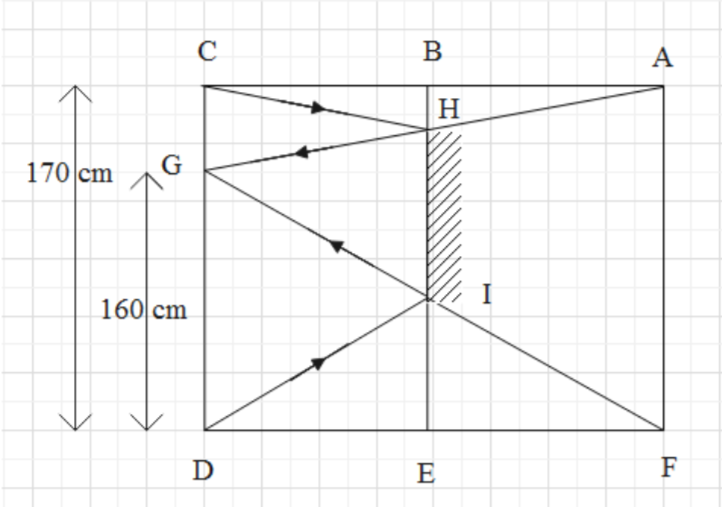
Consider the above figure while going through the following steps.
From the figure, it’s clear that triangle AGF and triangle HGI are similar
\[\Delta AGF\sim \Delta HGI\]
So, we have,
\[\dfrac{AF}{HI}=\dfrac{2d}{d}\]
HI = 85 cm
Therefore, the minimum length of the mirror is 85 cm.
From the figure, it’s clear that triangle FGD and triangle FIE are similar
\[\Delta FGD\sim \Delta FIE\]
So, we have,
\[\dfrac{GD}{IE}=\dfrac{2d}{d}\]
IE = 80 cm
Therefore, the bottom of the mirror should be at a height of 80 cm or more.
As the value of the minimum length of the mirror obtained is 85 cm and the value of the bottom position of the mirror from the ground obtained is 80 cm, thus, option (B) and (C) are correct.

Note: The things to be on your finger-tips for further information on solving these types of problems are: The units of the parameters given in the question should be compared to that given in the options. It is better to go with an indirect method to get a clear understanding of the concept.