Question

A man observes a tower AB of height h from a point P on the ground. He moves a distance d towards the foot of the tower and finds that the angle of elevation is doubled. He further moves a distance \[\dfrac{3d}{4}\] in the same direction and finds that the angle of elevation is three times that of P.
Prove that \[36{{h}^{2}}=35{{d}^{2}}\] .

Answer 1

Hint: We start solving the problem by drawing the required triangle and finding all the angles required using the facts that the angle of a straight and sum of angles in a triangle is ${{180}^{o}}$. We then use sine rule that is as follows \[\dfrac{\sin A}{a}=\dfrac{\sin B}{b}=\dfrac{\sin C}{c}=k\] (Where A, B and C are the angles of vertices A, B and C respectively and a, b and c are the side lengths of the sides that are in front of the angles A, B and C respectively and k is some constant) to solve for the relations between sides. We then make the necessary arrangements and calculations to prove the required result.

Complete step-by-step answer:
As mentioned in the question, the figure would look like the below picture

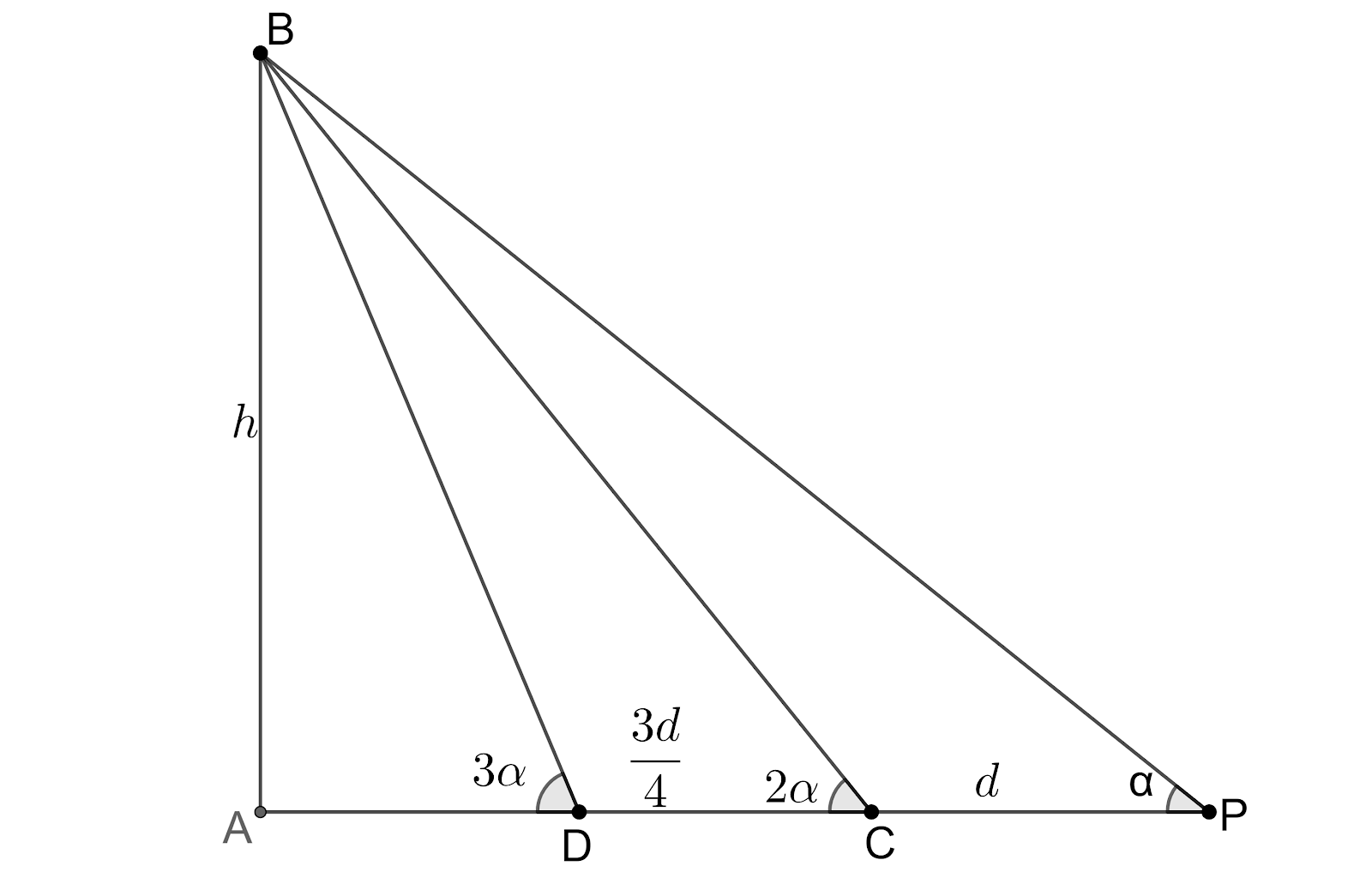
From the figure, we can see that $\angle PCB+\angle BCD=\pi $ as the angle of a straight line is ${{180}^{o}}$.
$\angle PCB+2\alpha =\pi $.
$\angle PCB=\pi -2\alpha $.
In \[\vartriangle BCP\] , we know that the sum of all angles in a triangle is ${{180}^{o}}$.
$\angle PCB+\angle CBP+\angle BCP=\pi $.
$\pi -2\alpha +\angle CBP+\alpha =\pi $.
$\pi -\alpha +\angle CBP=\pi $.
$\angle CBP=\pi -\pi +\alpha $.
$\angle CBP=\alpha $.
we can see that $\angle CDB+\angle BDA=\pi $ as the angle of a straight line is ${{180}^{o}}$.
$\angle CDB+3\alpha =\pi $.
$\angle CDB=\pi -3\alpha $.
Similarly, in $\Delta CDB$, we know that the sum of all angles in a triangle is ${{180}^{o}}$.
$\angle BCD+\angle CDB+\angle DBC=\pi $.
$\pi -3\alpha +\angle CBD+2\alpha =\pi $.
$\pi -\alpha +\angle CBD=\pi $.
$\angle CBD=\pi -\pi +\alpha $.
$\angle CBD=\alpha $.
Similarly, in $\Delta APB$, we know that the sum of all angles in a triangle is ${{180}^{o}}$.
$\angle BAP+\angle APB+\angle PBA=\pi $.
$\dfrac{\pi }{2}+\alpha +\angle PBA=\pi $.
$\angle PBA=\pi -\dfrac{\pi }{2}-\alpha $.
$\angle PBA=\dfrac{\pi }{2}-\alpha $.
Now, using the property of isosceles triangles, as \[\angle CBP=\angle BPC\], therefore, AC=d.
Now, let BD be x and we know that \[\angle ABD=\pi -3\alpha \] .
So, now, by applying sine rule in \[\vartriangle CBD\], we get
\[\dfrac{d}{sin(\pi -3\alpha )}=\dfrac{3d}{4sin\alpha }=\dfrac{x}{sin2\alpha }\].
\[\dfrac{d}{3sin\alpha -4si{{n}^{3}}\alpha }=\dfrac{3d}{4sin\alpha }=\dfrac{x}{2sin\alpha cos\alpha }\].
\[\dfrac{d}{3-4si{{n}^{2}}\alpha }=\dfrac{3d}{4}=\dfrac{x}{2\cos \alpha }\].
Now,
\[4d=3d(3-4si{{n}^{2}}\alpha )\].
\[4=9-12si{{n}^{2}}\alpha \].
\[12si{{n}^{2}}\alpha =5\].
\[si{{n}^{2}}\alpha =\dfrac{5}{12}\].
Now, we use the trigonometric identity,\[si{{n}^{2}}\alpha +{{\cos }^{2}}\alpha =1\].
So, \[{{\cos }^{2}}\alpha =1-\dfrac{5}{12}\].
\[{{\cos }^{2}}\alpha =\dfrac{7}{12}\] ---(1).
Now, using the other two terms of the sine rule equation, we get
\[\dfrac{3d}{4}=\dfrac{x}{2\cos \alpha }\].
\[3d\cos \alpha =2x\].
Squaring on both sides we get,
\[9{{d}^{2}}{{\cos }^{2}}\alpha =4{{x}^{2}}\].
Now we use the value of \[{{\cos }^{2}}\alpha \] obtained from equation (1).
\[9{{d}^{2}}\dfrac{7}{12}=4{{x}^{2}}\].
\[21{{d}^{2}}=16{{x}^{2}}\].
Now, another relation that we have is
\[\sin 3\alpha =\dfrac{h}{x}\].
\[3\sin \alpha -4{{\sin }^{3}}\alpha =\dfrac{h}{x}\].
\[\sin \alpha \left( 3-4{{\sin }^{2}}\alpha \right)=\dfrac{h}{x}\].
\[\sin \alpha \left( 3-4\times \dfrac{5}{12} \right)=\dfrac{h}{x}\].
\[\sin \alpha \left( 3-\dfrac{5}{3} \right)=\dfrac{h}{x}\].
\[\sin \alpha \left( \dfrac{9-5}{3} \right)=\dfrac{h}{x}\].
\[\sin \alpha \left( \dfrac{4}{3} \right)=\dfrac{h}{x}\].
Squaring on both sides, we get
\[{{\sin }^{2}}\alpha \dfrac{16}{9}=\dfrac{{{h}^{2}}}{{{x}^{2}}}\].
On putting the values of ${{x}^{2}}$ and ${{\sin }^{2}}\alpha $ we get,
\[\dfrac{5}{12}\times \dfrac{16}{9}=\dfrac{16{{h}^{2}}}{21{{d}^{2}}}\].
\[35{{d}^{2}}=36{{h}^{2}}\].
Hence, proved.

Note: We can make an error while drawing the figure and then end up doing mistakes which would get to the incorrect solution. Also, the calculation should be done very efficiently as there are very high chances of students committing a mistake in solving this question. We can also use that cosine rule in order to prove this result.