Question

A man observes a car from the top of a tower, which is moving towards the tower with a uniform speed. If the angle of depression of the car changes from $ 30^\circ $ to $ 45^\circ $ in $ 12 $ minutes. Find the time taken by the car now to reach the tower.

Answer 1

Hint: We can use the concept of trigonometric ratio. Drawing the diagram and finding which ratio will help to solve the question is the key.
Formula Required:
 $ {\text{tan}}\theta = \dfrac{{{\text{opposite side}}}}{{{\text{adjacent side}}}} $

 $
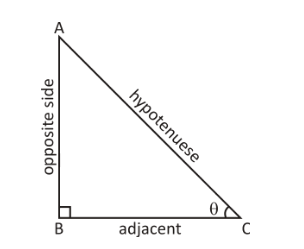
  \tan 30^\circ = \dfrac{1}{{\sqrt 3 }} \\
  \tan 45^\circ = 1 \\
  $
 $ \sqrt 3 = 1.732 $
Distance is the product of speed and time.

Complete step-by-step answer:
Given: man observes a car from the top of a tower
Car is moving at a uniform speed.
Angle of depression of the car changes from $ 30^\circ $ to $ 45^\circ $ in $ 12 $ minutes.
We need to find time taken by the car from second position to reach the bottom of the tower.
Let’s consider the below figure,

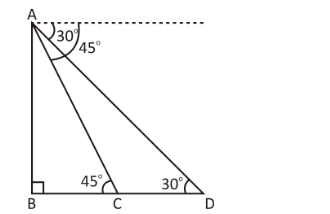
Where,
$ {\text{AB}} $ is the height of the tower
Initial position of the car is at $ {\text{D}} $
Next position of the car is at $ {\text{C}} $
 $ 30^\circ $ and $ 45^\circ $ are the angle of depressions of a car from the top of the tower.
Let $ {\text{CD}} = {{\text{d}}_1} $
 $ {\text{CB}} = {{\text{d}}_2} $
Time taken from $ {\text{D}} $ to $ {\text{C}} $ is $ {{\text{t}}_{\text{1}}} $
According to the question, $ {{\text{t}}_{\text{1}}} = 12 $ minutes.
Time taken from $ {\text{C}} $ to $ {\text{B}} $ is $ {{\text{t}}_2} $
From Triangle ABC,
 $
  {\text{tan45}}^\circ {\text{ = }}\dfrac{{{\text{opposite side to 45}}^\circ }}{{{\text{adjacent side to 45}}^\circ }} \\
   \Rightarrow {\text{tan45}}^\circ {\text{ = }}\dfrac{{{\text{AB}}}}{{{\text{BC}}}} \;
  $
We know that $ {\text{tan45}}^\circ = {\text{1}} $
 $
   \Rightarrow {\text{1}} = \dfrac{{{\text{AB}}}}{{{\text{BC}}}} \\
   \Rightarrow {\text{AB}} = {\text{BC}} \;
  $
 $ \Rightarrow {\text{AB}} = {\text{BC}} = {{\text{d}}_{\text{2}}} $ …………..Equation(1)
From Triangle ABD,
 $
  {\text{tan30}}^\circ {\text{ = }}\dfrac{{{\text{opposite side to 30}}^\circ }}{{{\text{adjacent side to 30}}^\circ }} \\
   \Rightarrow {\text{tan30}}^\circ = \dfrac{{{\text{AB}}}}{{{\text{BD}}}} \\
   \Rightarrow {\text{tan30}}^\circ = \dfrac{{{\text{AB}}}}{{{\text{BC + CD}}}} \;
  $
We know that $ {\text{tan30}}^\circ = \dfrac{{\text{1}}}{{\sqrt 3 }} $
 $ \Rightarrow \dfrac{{\text{1}}}{{\sqrt 3 }} = \dfrac{{{\text{AB}}}}{{{\text{BC + CD}}}} $
 $ \Rightarrow {\text{BC + CD}} = \sqrt 3 {\text{AB}} $ …………..Equation(2)
Substituting Equation(1) in Equation(2) we get,
 $ \Rightarrow {{\text{d}}_{\text{2}}} + {{\text{d}}_{\text{1}}} = \sqrt {\text{3}} {{\text{d}}_{\text{2}}} $ ( $ {\text{CD = }}{{\text{d}}_1} $ and $ {\text{CB = }}{{\text{d}}_2} $ ) ……….Equation(3)
Distance is the product of speed and time.
 $
   \Rightarrow {{\text{d}}_{\text{1}}}{\text{ = }}{{\text{s}}_{\text{1}}} \times {{\text{t}}_{\text{1}}} \\
   \Rightarrow {{\text{d}}_{\text{1}}}{\text{ = s}} \times {\text{12}} \\
  $
Similarly,
 $
   \Rightarrow {{\text{d}}_{\text{2}}} = {{\text{s}}_{\text{2}}} \times {{\text{t}}_{\text{2}}} \\
   \Rightarrow {{\text{d}}_{\text{2}}} = {\text{s}} \times {{\text{t}}_{\text{2}}} \\
  $
Since the car travels with uniform speed $ {{\text{s}}_{\text{1}}} = {{\text{s}}_{\text{2}}} = {\text{s}} $
Now substituting the values of $ {{\text{d}}_{\text{1}}} $ and $ {{\text{d}}_2} $ in equation (3) we get,
\[
   \Rightarrow {{\text{d}}_{\text{2}}} + {{\text{d}}_{\text{1}}} = \sqrt {\text{3}} {{\text{d}}_{\text{2}}} \\
   \Rightarrow {\text{s}} \times {{\text{t}}_2} + {\text{s}} \times 12{\text{ = }}\sqrt {\text{3}} \left( {{\text{s}} \times {{\text{t}}_2}} \right) \\
   \Rightarrow {{\text{t}}_2} + 12{\text{ = }}\sqrt {\text{3}} \times {{\text{t}}_2} \\
   \Rightarrow \left( {\sqrt {\text{3}} - 1} \right){{\text{t}}_2} = 12 \\
   \Rightarrow {{\text{t}}_2} = \dfrac{{12}}{{\sqrt {\text{3}} - 1}}
 \]
Approximating $ \sqrt 3 = 1.732 $ we get,
 $ {{\text{t}}_{\text{2}}} = {\text{16}}{\text{.39}} $ Minutes.
Therefore time taken by the car from second position to reach the bottom of the tower is $ {\text{16}}{\text{.39}} $ minutes.
So, the correct answer is “ $ {\text{16}}{\text{.39}} $ minutes”.

Note: In the questions involving heights and distances concept the diagram leads to forming right triangles, In that case the questions tests us about the trigonometric ratios. We need to have an idea about the definition of trigonometric ratios and the values of angle of the same. As per the data given in the question we need to figure out which ratio will help us to find the answer.