Question

A man is walking at a speed 3m/s, raindrops are falling at a speed of 3m/s:
i) What is the velocity of rain drop with respect to the man?
ii) At what angle from vertical, the man should hold his umbrella?
A) 2.42 m/s, 30°in forward direction
B) 4. 24 m/s, 45°in forward direction
C) 1. 24 m/s, 60°in forward direction
D) None of the above

Answer 1

Hint:
We can identify the direction of man and rain with respect to their axes and carry out a relationship between the two velocities.

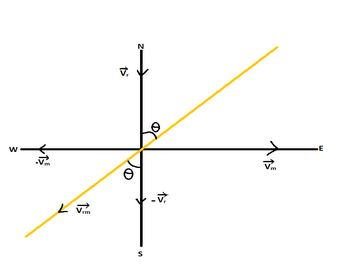
The angle at which the umbrella should be held can be given by:
$\tan \theta = \dfrac{{perpendicular}}{{base}}$
Calculating velocity of an object A with respect to B:
${V_{AB}} = {V_A} - {V_B}$
Calculating the magnitude of a vector:
$x\hat i + y\hat j = \sqrt {{{\left( x \right)}^2} + {{\left( y \right)}^2}} $

Complete step by step answer:
The man is walking in the positive direction of x – axis:
${V_m}$= $\overrightarrow {{V_m}} $
$\overrightarrow {{V_m}} $ = 3 $\hat i$ m/s (given)
The rain is coming downwards, it is in the negative direction of y – axis:
${V_r}$= $ - \overrightarrow {{V_r}} $
$\overrightarrow {{V_r}} $ = - 3 $\hat j$ m/s (given)

i) The velocity of man with respect to rain is:
${V_{rm}} = {V_r} - {V_m}$
$\overrightarrow {{V_{rm}}} = \overrightarrow {{V_r}} - \overrightarrow {{V_m}} $
Substituting the values:
\[\overrightarrow {{V_{rm}}} = - 3\hat i - 3\hat j\]
Calculating the magnitude of this vector:
\[
  {V_{rm}} = \sqrt {{{( - 3)}^2} + {{( - 3)}^2}} \\
  \Rightarrow {V_{rm}} = \sqrt {18} \\
  \Rightarrow {V_{rm}} = 3\sqrt 2 \\
 \]
$3\sqrt 2 \approx 4.24$
Therefore, the velocity of man with respect to rain is 4.24 m/s

ii) Angle at which the man should hold his umbrella:
if we calculate $\tan \theta $, from the figure:
$
  \tan \theta = \dfrac{{perpendicular}}{{base}} \\
  \tan \theta = \left| {\dfrac{{{V_r}}}{{{V_m}}}} \right| \\
 $
Substituting the values:
$
  \Rightarrow \tan \theta = \left| {\dfrac{{ - 3}}{{ - 3}}} \right| \\
  \Rightarrow \tan \theta = \dfrac{3}{3} \\
  \Rightarrow \tan \theta = 1 \\
 $
Calculating the value of $\theta $:
$
  \Rightarrow \tan \theta = 1 \\
  \Rightarrow \theta = {\tan ^{ - 1}}(1) \\
 $
$\tan \theta = 1$, at 45°, so:
$\Rightarrow \theta $ = 45°
Therefore, the man should hold the umbrella at 45° in forward direction so as to not get wet.
Thus, the correct option is B) 4. 24 m/s, 45° in forward direction.

Note:We use $\left| {} \right|$ sign represents magnitude, it is always positive even for the negative values because negative sign shows only direction and the magnitude only refers to the value.
$\hat i$ and $\hat j$ are called unit vectors representing the quantity along x and y axes respectively.