Question

A man is travelling on the road along $AB$, find out the length road for which the image will be visible to him:

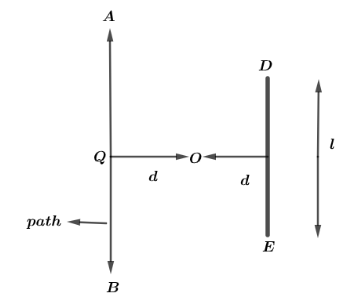
A. $l$
B. $3l$
C. $1.5l$
D. $2l$

Answer 1

Hint: We can solve this question by tracing the light ray’s path and form an image behind the plane mirror $DE$ and hence will find the length of $AB$ and will use simple geometry of congruent triangles. Image due to a plane mirror is always formed behind the mirror.

Complete step by step answer:
Let us first draw the ray diagram of the given question. Draw a light ray from $O$ to $D$ and $O$ to $E$. Let $M$ be the mirror and let triangle $AQR$ and $DMR$.
Both are right angled triangles and angle $ < R$ is common in them which shows,
Both triangles are congruent and hence, using the ratio of sides we get,
$\dfrac{{AQ}}{{DM}} = \dfrac{{QR}}{{MR}} \to (i)$
Now, the side $AQ$ is half of the total side $2x$ which implies that
$AQ = x$
And side $DM$ is half of the total side $l$ which implies that,

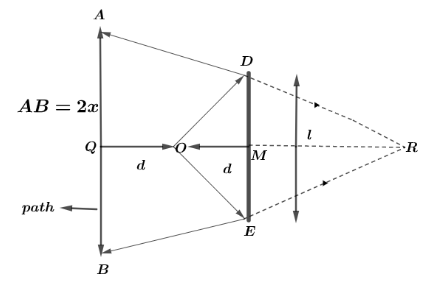
$DM = \dfrac{l}{2}$
From diagram we also know,
$QR = 3d$ As distance $MR = d$ because object $O$ lies at a distance of $d$ from the mirror $M$
So, $MR = d$ .
Now, we will put these values in the equation $(i)$. We get,
$\dfrac{{2x}}{l} = 3$
$\Rightarrow x = \dfrac{{3l}}{2}$
But, we need to find the length of
$AB = 2x$
$\therefore AB = 3l$
So the distance of the road must be of length $3l$ in order to form a full image through the mirror.

Hence, the correct option is B.

Note: Remember, the condition for the congruence of two right angle triangle is such that, both must be right angles triangle and an angle other than ${90^ \circ }$ must be equal, than both triangles will be congruent and every congruent triangles are similar hence their ratio of side will be equal.