Question

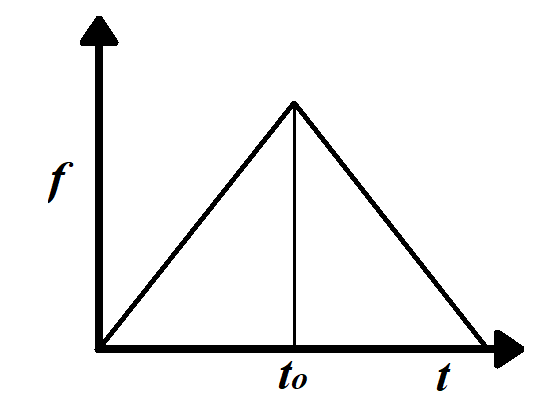
A man is standing on a railway platform listening to the whistle of an engine that passes the man at constant speed without stopping. If the engine passes the man at time ${{t}_{o}}$. How does the frequency f of the whistle as heard by the man change with time?
A.
     

B.
     

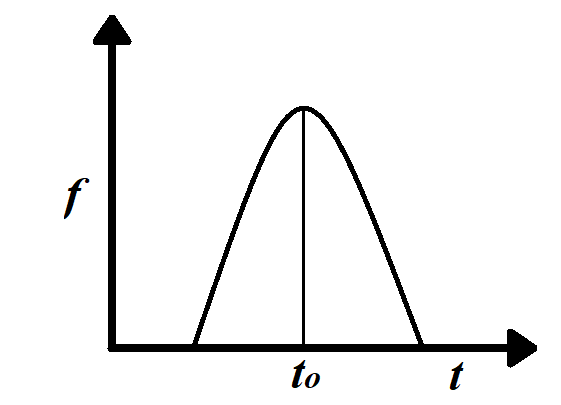
C.
     

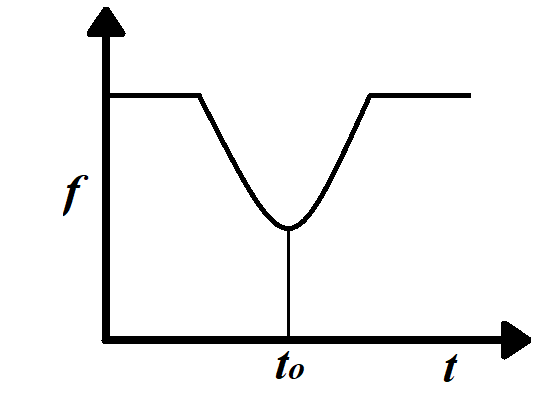
D.
     

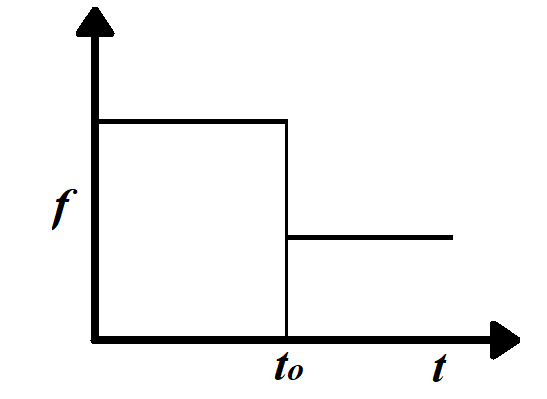
Answer 1

Hint: The Doppler Effect or the Doppler shift is used to describe the change in frequency of any kind of sound or light wave produced by a moving source with respect to an observer. We can apply the equation of apparent frequency heard by the observer and determine the relation between original frequency, apparent frequency and the time. The above relation will help us choose the correct graph representing the frequency heard by man and its variation with the time.

Complete step by step answer:
Doppler Effect is described as an increase, or decrease, in the frequency of sound, light, or other waves as the source and the observer move towards or away from each other.
The waves emitted by a source travelling towards an observer get compressed, while in contrast, the waves emitted by a source travelling away from an observer get stretched out. The apparent change in the frequency of sound due to the relative motion between the source of the sound and the observer is known as the Doppler Effect.
The apparent frequency for different can be calculated as follows:
When both observer and source are at rest
Let’s consider $\eta $ be the frequency of sound and $v$ be the velocity of sound.
In this case, the frequency heard by the observer will be the same as the frequency of the sound wave emitted by the source.
$\eta '=\eta $
$\eta '$ is the apparent frequency heard by the observer
$\eta $ is the original frequency of sound emitted by the source
When the source is in motion and observer at rest
a) If the source moves towards the stationary observer with velocity ${{v}_{s}}$
In this case, the apparent frequency heard by the observer is given by,
$\eta '=\left( \dfrac{v}{v-{{v}_{s}}} \right)\eta $
Where,
$\eta '$ is the apparent frequency heard by the observer
$v$ is the velocity of sound in air or vacuum
${{v}_{s}}$ is the velocity of source
$\eta $ is the original frequency of sound emitted by the source
b) If the source moves away from the stationary observer with velocity${{v}_{s}}$
In this case, the apparent frequency heard by the observer is given by,
$\eta '=\left( \dfrac{v}{v+{{v}_{s}}} \right)\eta $
Where,
$\eta '$ is the apparent frequency heard by the observer
$v$ is the velocity of sound in air or vacuum
${{v}_{s}}$ is the velocity of source
$\eta $ is the original frequency of sound emitted by the source
When the source is at rest and observer in motion
a) When the observer moves towards the stationary source with velocity ${{v}_{o}}$
In this case, the apparent frequency of sound heard by the observer is given by,
$\eta '=\left( \dfrac{v+{{v}_{o}}}{v} \right)\eta $
Where,
$\eta '$ is the apparent frequency heard by the observer
$v$ is the velocity of sound in air or vacuum
${{v}_{o}}$ is the velocity of source
$\eta $ is the original frequency of sound emitted by the source
b) When the observer moves away from the stationary source with velocity ${{v}_{o}}$
In this case, the apparent frequency of sound heard by the observer is given by,
$\eta '=\left( \dfrac{v+{{v}_{o}}}{v} \right)\eta $
Where,
$\eta '$ is the apparent frequency heard by the observer
$v$ is the velocity of sound in air or vacuum
${{v}_{o}}$ is the velocity of source
$\eta $ is the original frequency of sound emitted by the source
If the source and the observer move along the same direction, the equation for apparent frequency is given by the equation:
$\eta '=\left( \dfrac{v-{{v}_{o}}}{v-{{v}_{s}}} \right)\eta $
Where,
$\eta '$ is the apparent frequency heard by the observer
$v$ is the velocity of sound in air or vacuum
${{v}_{o}}$ is the velocity of source
${{v}_{s}}$ is the velocity of the source
$\eta $ is the original frequency of sound emitted by the source
We are given that a man is standing on a railway platform listening to the whistle of an engine that passes the man at constant speed without stopping,
When the train is approaching the stationary observer,
Apparent frequency heard by the observer is given by,
$\eta '=\left( \dfrac{v}{v-{{v}_{t}}} \right)\eta $
Where,
$\eta '$ is the apparent frequency heard by the observer
$v$ is the velocity of sound in air or vacuum
${{v}_{s}}$ is the velocity of train engine
$\eta $ is the original frequency of sound emitted by the source train
When the train is moving away from the stationary observer,
 Apparent frequency heard by the observer is given by,
$\eta ''=\left( \dfrac{v}{v-{{v}_{t}}} \right)\eta $
Where,
$\eta '$ is the apparent frequency heard by the observer
$v$ is the velocity of sound in air or vacuum
${{v}_{s}}$ is the velocity of train engine
$\eta $ is the original frequency of sound emitted by the source train
Frequencies $n'$ and $n''$ are independent of time.
Also, $n' > n''$
Apparent frequency heard by an observer while the train is approaching him is greater than the frequency heard by the observer while the train is moving from him. Both the frequencies are independent of time.
Hence, the correct option is D.

Note:
The Apparent change in the frequency of sound when the source, the observer and the medium are in a relative motion is called the Doppler Effect. It should be noted that the apparent frequency will be greater than the original frequency if the relative distance, or simply distance, between the source and the observer is decreasing, while the apparent frequency is smaller than the original frequency if the relative distance between the source and the observer is increasing.