Question

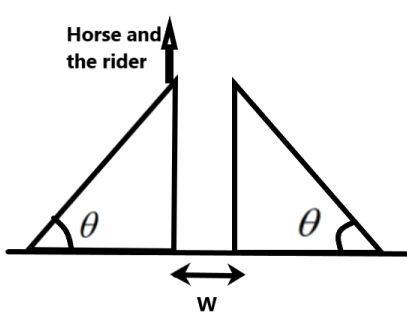
A man is riding on a horse. He is trying to jump the gap between two symmetrical ramps of snow separated by a distance W as shown in the figure. He launches off the first ramp with a speed \[{{V}_{L}}\]. The man and the horse have a total mass m and their size is small as compared to W. The initial launch speed of \[{{V}_{L}}\] which will put the horse exactly at the peak of the second ramp is –
          

\[\begin{align}
  & \text{A) }\sqrt{\dfrac{Wg}{\cos \theta \times \sin \theta }} \\
 & \text{B) }\sqrt{\dfrac{Wg}{\sin (\dfrac{\theta }{2})\times \cos (\dfrac{\theta }{2})}} \\
 & \text{C) }\sqrt{\dfrac{Wg}{2\sin \theta \cos \theta }} \\
 & \text{D) }\sqrt{\dfrac{2Wg}{\sin \theta \cos \theta }} \\
\end{align}\]

Answer 1

Hint: We need to understand the laws of motion and its approach in a projectile motion. The horse and the rider must land on the second ramp if they possess the required velocity which we are to calculate from the data given from the problem.

Complete answer:
We are to calculate the velocity with which a system of masses consisting of a horse and the rider to safely land on a ramp which is at a gap of W from their initial position as we can see in the figure.

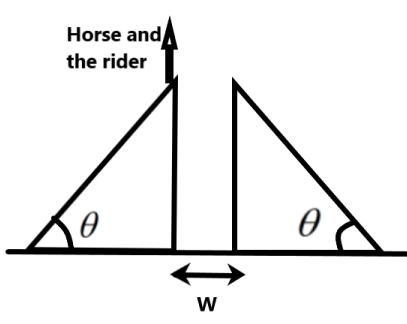
We can understand from the figure that the gap between the ramps is the range of the horizontal motion. The motion of the horse and the rider from the first ramp to the second ramp is a portion of projectile motion with an angle of projection \[\theta \].
  

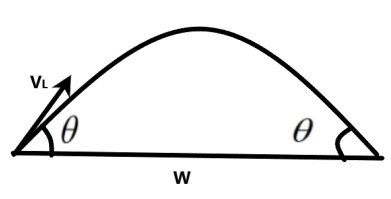
We know in the projectile motion we can find the range as –
\[R=\dfrac{{{u}^{2}}\sin 2\theta }{g}\]
Where, u is the initial velocity and R is the range of projectile.
In the situation given,
The initial velocity is \[{{V}_{L}}\] and the range is W. We can find the initial velocity from the above relation as –
\[\begin{align}
  & R=\dfrac{{{u}^{2}}\sin 2\theta }{g} \\
 & \Rightarrow W=\dfrac{{{v}_{L}}^{2}\sin 2\theta }{g} \\
 & \Rightarrow W=\dfrac{{{v}_{L}}^{2}2\sin \theta \cos \theta }{g} \\
\end{align}\]
\[\begin{align}
  & \Rightarrow {{v}_{L}}^{2}=\dfrac{Wg}{2\sin \theta \cos \theta } \\
 & \therefore {{v}_{L}}=\sqrt{\dfrac{Wg}{2\sin \theta \cos \theta }} \\
\end{align}\]
The initial velocity of the horse and the man to safely land on the second ramp is given above.

The correct answer is option C.

Note:
The range of a projectile motion is the horizontal distance covered by an object in the motion. It is dependent on the initial velocity and the angle of projection. We can observe that the mass of the system is not dependent on the range of the projectile.