Question

A man is on a ship which is moving in the east direction with speed\[{\text{60 km/hr}}\]. Waves of ocean are taking the ship towards west with speed\[{\text{20 Km/hr}}\]. Man starts running on ship with flag in hand in north direction with speed \[{\text{30 Km/hr}}\] and wind is blowing with\[{\text{50 Km/hr}}\] , \[{37^ \circ }\]towards south of west then find the direction of flutter the flag as seen by the man on the ground.
$(A)$ \[{37^ \circ }{\text{south of west}}\]
$(B)$ \[{53^ \circ }{\text{south of west}}\]
$(C)$ \[{\text{3}}{{\text{7}}^{\text{o}}}{\text{West of North}}\]
$(D)$ The flag will not flutter

Answer 1

Hint:This question is based on motion in a plane or motion in two dimensions. To solve this problem one must be aware of the directions and also about resultant vectors. By drawing the figure on an XY axis, one can help one to solve this question more easily. By mentioning the positive X-axis as East direction and positive Y-axis as North direction, one can draw the required diagram. By using this diagram and by finding the resultant, one can solve this problem.

Formula Used:
Resultant vector, $R = \sqrt {{x^2} + {y^2}} $ ; $\theta = {\tan ^{ - 1}}(\dfrac{y}{x})$


Complete step-by-step solution:
Using the given data, draw the graph on an XY plane. Let the positive x-axis represents the east direction, the negative x-axis represents the west direction, the positive y-axis represents the North direction and the negative y-axis represents the east direction.

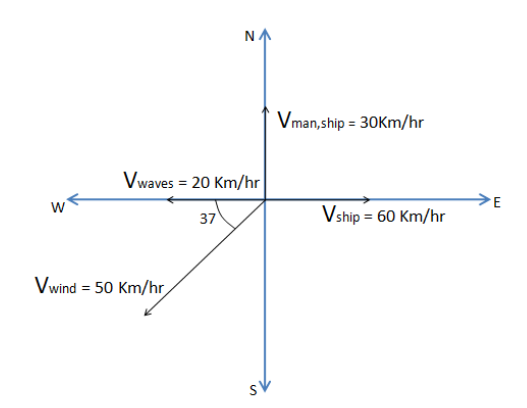
The velocity of the ship with respect to ground will be equal to the velocity of the ship subtracted with the velocity of the wave.
Mathematically,${\overrightarrow {\text{V}} _{{\text{ship,ground}}}}{\text{ = 60 Km/hr - 20 Km/hr}}$
Simplifying we get, ${\overrightarrow {\text{V}} _{{\text{ship,ground}}}}{\text{ = 40 Km/hr }}$
This is represented in the graph drawn below.
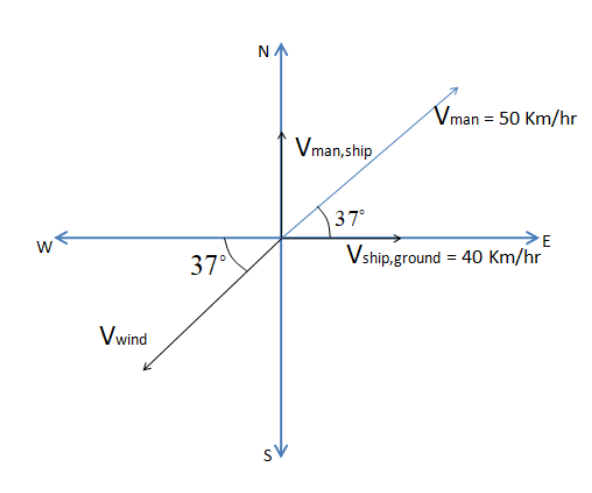
Now, the resultant in the positive XY plane will help us to determine the velocity of the man with respect to the ground.
${\overrightarrow {\text{V}} _{{\text{man,ship}}}}{\text{ = }}{\overrightarrow {\text{V}} _{{\text{man}}}}{\text{ - }}{\overrightarrow {\text{V}} _{{\text{ship}}}}$
In vector form; ${\overrightarrow {\text{V}} _{{\text{man,ship}}}}{\text{ = 30j}}$ (y-axis is represented in the unit vector format$j$ )
${\overrightarrow {\text{V}} _{{\text{ship}}}} = 40i$ (X-axis is represented in the unit vector format \[i\] )
By substituting this value in the above expression, we can obtain the velocity of the man with respect to the ground.
${\overrightarrow {\text{V}} _{{\text{man,ship}}}}{\text{ = }}{\overrightarrow {\text{V}} _{{\text{man}}}}{\text{ - }}{\overrightarrow {\text{V}} _{{\text{ship}}}}$
${\text{30j = }}{\overrightarrow {\text{V}} _{{\text{man}}}}{\text{ - 40i}}$
Rearranging we get, ${\overrightarrow {\text{V}} _{{\text{man}}}}{\text{ = 40i + 30j}}$
The magnitude of the velocity of the man with respect to ground can be obtained using the resultant formula$R = \sqrt {{x^2} + {y^2}} $
${V_{man}} = \sqrt {{{40}^2} + {{30}^2}} $
Solving this we get, ${V_{man}} = 50$
Now to calculate the angle we can use the expression; $\theta = {\tan ^{ - 1}}(\dfrac{y}{x}) = {\tan ^{ - 1}}(\dfrac{{30}}{{40}})$
Simplifying we get, $\theta = {\tan ^{ - 1}}(0.75) = {37^ \circ }$north of East
This is represented in the diagram given below

Now the velocity of wind with respect to the man with respect to the ground is equal to the velocity of wind with respect to the ground subtracted with the velocity of the man with respect to the ground,
${{\text{V}}_{{\text{wind,manground}}}} = {{\text{V}}_{{\text{wind,ground}}}} - {{\text{V}}_{{\text{man,ground}}}}$
${{\text{V}}_{{\text{wind,manground}}}} = 50 - ( - 50) = 100{\text{Km/hr}}$ (The negative sign is from when the vector is rotated)
This can be seen in the diagram given below.

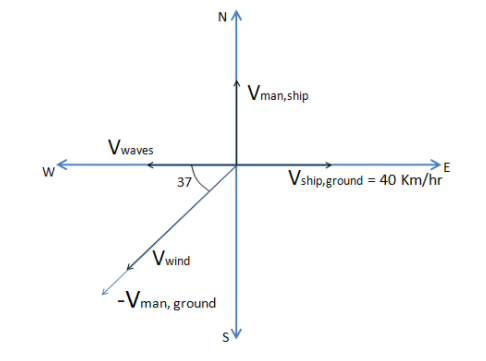
Therefore the direction of flutter of the flag is ${37^ \circ }{\text{south of west}}$
From the solution, we have obtained option $(A)$ to be the correct option

Note:Vectors are those quantities that have both direction and magnitude. These vectors, if they are in the same direction we can add them, if, in the opposite direction, they will be subtracted. If the direction of a vector is changed by ${180^ \circ }$, then its magnitude will have a negative sign. To calculate the resultant of a vector, one must find the square root of the sum of squares of individual vectors.