Question

A man is 40 m behind the bus when the bus starts accelerating from rest with acceleration \[1.25\,m{s^{ - 2}}\]. With what minimum velocity should the man start running to catch the bus?
A. 15
B. 20
C. 10
D. 12

Answer 1

Hint: This question can be easily solved by Newton's second equation of motion for uniform acceleration. For a man to catch the bus the distance covered by the man should be 40m more than the distance covered by the bus at the instant when he catches the bus. By applying this condition we can easily calculate the required velocity to catch the bus.

Complete step by step answer:
Equations of motion are physics equations that define a physical system's action in terms of its motion as a function of time. The equations of motion, more precisely, describe the behaviour of a physical system as a sequence of mathematical functions expressed in terms of dynamic variables.

Given, $u = 0\,m/s$, acceleration of bus = \[1.25\,m{s^{ - 2}}\]
Using 2nd equation of motion
\[{\text{s}} = {\text{ut}} + \dfrac{1}{2}{\text{a}}{{\text{t}}^2}\]
Substituting the values of u and a
\[{\text{s}} = 0 + \dfrac{1}{2} \times 1.{\mathbf{25}}{{\mathbf{t}}^{\mathbf{2}}}\]
\[\Rightarrow {\text{s}} = \dfrac{{1.{\mathbf{25}}}}{2}{{\text{t}}^2} \ldots \ldots \ldots {\text{ (1) }}\]
Let us consider, $u$ be initial velocity of man

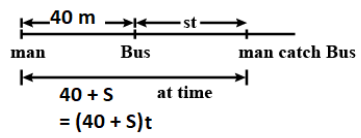
Now the man needs to cover a distance of (40+s)m at time t to catch the bus
\[{\mathbf{ut}} = {\mathbf{4}}0 + {\mathbf{s}}\]
From eqn 1
\[{\text{ut}} = 40 + \dfrac{{1.25}}{2}{{\text{t}}^2}\]
\[\Rightarrow {\mathbf{u}} = \dfrac{{40}}{{\text{t}}} + 1.25{\text{t}} \ldots \ldots \ldots {\text{ (2) }}\]

For minimum velocity,
\[{\dfrac{{{\text{du}}}}{{{\text{dt}}}} = 0}\]
\[\Rightarrow { - \dfrac{{40}}{{{{\text{t}}^2}}} + 0.625 = 0}\]
\[\Rightarrow {40 = 0.625{{\text{t}}^2}}\]
\[\Rightarrow {{\text{0}}{\text{.625}}{{\text{t}}^2} = 40}\]
\[\Rightarrow {{{\text{t}}^2} = \dfrac{{40}}{{0.625}} = 64}\]
\[\Rightarrow {{\text{t}} = 8{\text{s}}}\]
From eqn 2
\[{{{\text{u}}_{\min }} = \dfrac{{40}}{8} + 0.625 \times 8}\]
\[\Rightarrow {{{\text{u}}_{\min }} = 5 + 5}\]
\[\therefore {{{\text{u}}_{\min }} = 10\;{\text{m}}/{\text{s}}}\]

Hence, the correct answer is option C.

Note: According to the first law, until a force acts on an entity, it can not alter its motion. The force on an object is proportional to its mass times its acceleration, according to the second law. When two objects meet, the third rule states that they apply forces of equal magnitude and opposite direction to each other.