Question

A man is $24$ years older than his son. $12$ years ago, he was five times as old as his son. Find the present ages of both.
A. Present age of father is $44$ years and present age of son is $20$ years.
B. Present age of father is $42$ years and present age of son is $18$ years.
C. Present age of father is $60$ years and present age of son is $36$ years.
D. Present age of father is $48$ years and present age of son is $24$ years.

Answer 1

Hint: For this problem we need to find the age of son and father according to the given conditions. So, we will first assume the age of the father as $x$ and son as $y$. Now we will consider the given condition that the man is $24$ years older than his son. From this we can obtain an equation in the two variables. After that we will consider the second equation that $12$ years ago, he was five times as old as his son. From this condition we can obtain another equation in terms of two variables. Now we will solve both the equations to get the required result.

Complete step-by-step solution:
Let the age of the man or father is $x$ years.
Age of the son is $y$ years.
Given that, the man is $24$ years older than the son, so we can write the difference of the ages as $24$. Then we can write
$\Rightarrow x-y=24.....\left( \text{i} \right)$
Again, we have that $12$ years ago, he was five times as old as his son.
$12$ years ago, the ages of father and son will be $x-12$, $y-12$. Now we can write the equation as
$\Rightarrow x-12=5\left( y-12 \right)$
Simplifying the above equation, then we will get
$\begin{align}
  & \Rightarrow x-12=5y-60 \\
 & \Rightarrow x-5y=-48....\left( \text{ii} \right) \\
\end{align}$
To solving the both the equations we are going to subtract the equation (ii) from (i), then we will get
$\Rightarrow x-y-\left( x-5y \right)=24-\left( -48 \right)$
Simplifying the above equation, then we will have
$\begin{align}
  & \Rightarrow x-y-x+5y=24+48 \\
 & \Rightarrow 4y=72 \\
\end{align}$
Dividing the above equation with $4$ on both sides, then we will get
$\begin{align}
  & \Rightarrow \dfrac{4y}{4}=\dfrac{72}{4} \\
 & \Rightarrow y=18 \\
\end{align}$
Hence the age of the son is $18$ years.
From equation $\left( \text{i} \right)$ the age of father will be
$\begin{align}
  & \Rightarrow x=18+24 \\
 & \Rightarrow x=42 \\
\end{align}$
Hence the age of the father is $42$ years.

Note: We can also solve the obtained two equations by using the graphical method in which we will plot the given equations in a coordinate system and observe the intersection point of the two lines and write it as the solution of the equation. When we plot the graph of the obtained equations, then we will get

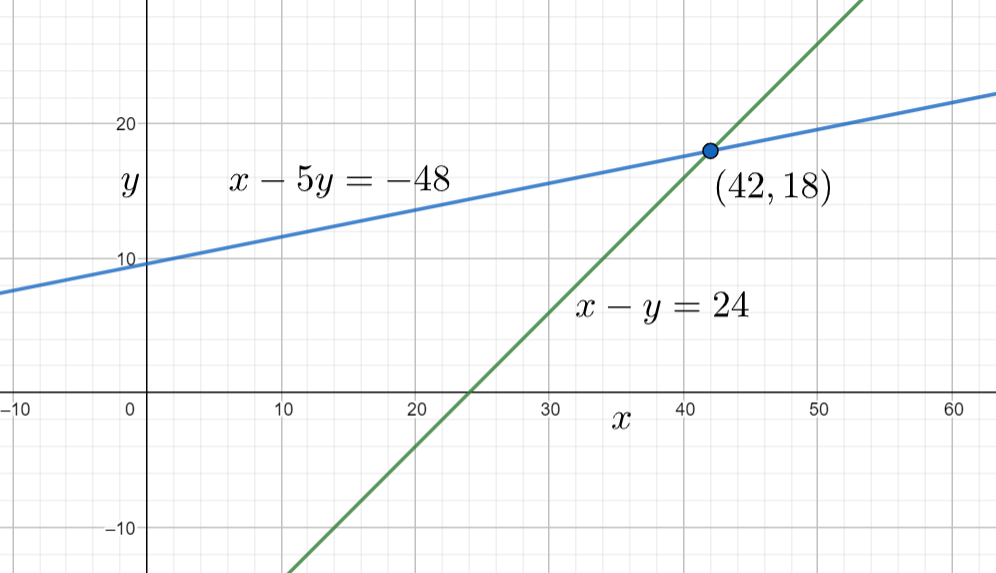
From the above graph also, we can say that the solution of the two equations is $x=42$, $y=18$.