Question

A man in a balloon rising vertically with an acceleration of 4.9m/s² releases a ball 2 second after the balloon is let go from the ground. The greatest height above the ground reached by the ball is: (g=9.8m/s²)
A. $14.7m$
B. $19.6m$
C. $9.8m$
D. $24.5m$

Answer 1

Hint: To solve the above problem we should know the formulae for the motion. First formula is the velocity formula which will be use, that is $v = u + at$ and the second formula is the distance formula, that is $S = ut + \dfrac{1}{2}a{t^2}$, and the third formula is ${v^2} = {u^2} - 2as$.

Complete answer:
Firstly, we will prepare a diagram depicting the above scenario given in the question.
So, the diagram is as follows,

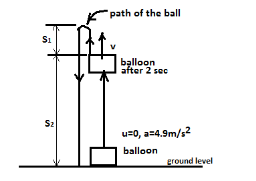
Given,
Initial velocity, $u = 0$m/s
Initial acceleration, $a = 4.9$m/s²
Time of fight, $t = 2\sec $
Let the velocity of the balloon after 2 second be $v$, then we will find the value of this velocity by using the formula,
$v = u + at$
Now putting the values in the above equation-
$ \Rightarrow v = 0 + (4.9 \times 2)$
$ \Rightarrow v = 9.8$m/s
So when the velocity of the balloon is 9.8 m/s then the ball is released, so due to this velocity of the balloon the ball will also travel some distance in the vertical upward direction and let us take that distance as ${S_1}$.
So the initial velocity of the ball will be the same as that of the velocity of the balloon after 2 second, and the ball will be under acceleration due to gravity and the final velocity will be zero when the ball will cover the distance ${S_1}$.
So, applying the formula,
${v^2} = {u^2} - 2as$,
Now putting all the values,
$ \Rightarrow 0 = {(9.8)^2} - 2(9.8){S_2}$ (since, $a = g = 9.8$m/s²)
$ \Rightarrow \dfrac{{9.8}}{2} = {S_1}$
$ \Rightarrow {S_1} = \dfrac{{9.8}}{2} = 4.9$
$ \Rightarrow {S_1} = 4.9m$
Now we will calculate the distance ${S_2}$.
This distance will be the same as the distance travelled by the balloon in 2 seconds.
So, for that we will use the formula,
$S = ut + \dfrac{1}{2}a{t^2}$
$ \Rightarrow {S_2} = 0 \times 2 + \dfrac{1}{2} \times 4.9 \times {(2)^2}$
$ \Rightarrow {S_2} = \dfrac{1}{2} \times 4.9 \times 4$
$ \Rightarrow {S_2} = 4.9 \times 2$
$ \Rightarrow {S_2} = 9.8m$
So, now the greatest height above the ground reached by the ball= ${S_1} + {S_2}$
$ = (4.9m + 9.8m) = 14.7m$

So, the correct answer is “Option A”.

Note:
- Here the ball was in vertical motion under gravity. In a vertical motion under gravity is a specific case of the linear motion under constant acceleration. At the highest point in a vertical motion under gravity the velocity of the ball is zero. Acceleration is always directed in a vertically downward direction. So, the ball will be under the force of gravity. For calculations we take the point of the release as origin and upward direction as positive.