Question

A man can swim in still water with a velocity of 5 meters per second. He wants to reach the direct opposite point on the other hand of a river which is flowing at a rate of 4 meters per second. The river is 15 meters wide, and the man can run with twice the velocity as compared with the velocity of the swimmer with respect to the river. If he swims perpendicular to river flow and then runs along the bank. Time, in seconds, taken by him to reach the opposite point is
A. 4.0
B. 4.2
C. 5.4
D. 3.6

Answer 1

Hint: In the question, we need to determine the total time taken by the man to reach the directly opposite point of the river by swimming and running. For this, we will use the basic relation between the distance, time, and velocity as $d = vt$ in both situations.

Complete step by step answer:
From the information given in the question, a rough sketch has been drawn for the displacement of the man at the time of swimming as well as the time of running.

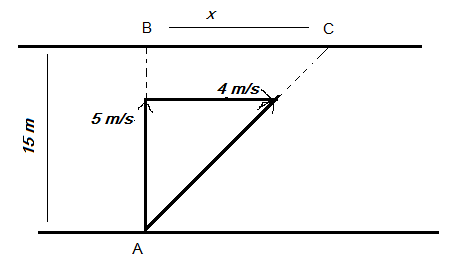
It is given in the question that the man swims perpendicular to the direction of the water flow, and so, due to relative motion, the man on swimming instead of reaching at point B directly, he approaches to point C from where he runs to reach point C.

Time taken by the man while swimming to reach at point C is given as \[{t_s} = \dfrac{d}{{{v_m}}}\].
So, substitute $d = 15{\text{ m}}$and ${v_m} = 5{\text{ m/s}}$ in the formula \[{t_s} = \dfrac{d}{{{v_m}}}\] to determine the time taken by the man to reach on the other bank.

\[
  {t_s} = \dfrac{d}{{{v_m}}} \\
   = \dfrac{{15}}{5} \\
   = 3{\text{ seconds}} - - - - (i) \\
 \]

According to the question, the man runs from C to B with double the speed with which he swims so, the velocity of the man while running is $v = 2 \times 5 = 10{\text{ m/s}}$.

Let us consider the distance between points B and C be $x$.
Now, to calculate the distance between points B and C, use the relation between the distance, velocity of water, and time as $x = {v_w}{t_s}$ where ${v_w} = 4{\text{ m/s}}$ is the velocity of the water and ${t_s} = 3{\text{ sec}}$ is the time when the man swims.

So, the distance between points B and C is determined as:

$
  x = {v_w}{t_s} \\
   = 4 \times 3 \\
   = 12{\text{ m}} \\
 $

Now, substitute $x = 12{\text{ m}}$and $v = 10{\text{ m/s}}$ in the formula ${t_r} = \dfrac{{{d_{BC}}}}{{{v_w}}}$ to determine the time taken by the man to run at point B from point C.

$
  {t_r} = \dfrac{{{d_{BC}}}}{{{v_w}}} \\
   = \dfrac{{12}}{{10}} \\
   = 1.2{\text{ seconds}} - - - - (ii) \\
 $

So, the total time taken by the man to reach from the point A to the point B, which is directly opposite to A, is given as the summation of the time taken by the man to swim from the point A to the point C and then run from the point C to the point B.

$
  t = {t_s} + {t_r} \\
   = 3 + 1.2 \\
   = 4.2{\text{ seconds}} \\
 $

Hence, the time taken by the man to cross the river is 4.2 seconds.
Option B is correct.

Note: Students should note here that the in the question, it is already been mentioned that the man swims perpendicular to the flow of the river and so he reaches to the point C due to the flow of the water in the river.