Question

A man $2{\text{m}}$ tall, whose eye level is ${\text{1}} \cdot {\text{84m}}$ above the ground, looks at his image in a vertical mirror. Find the minimum vertical length of the mirror so that the man can see the whole of himself.
A) ${\text{0}} \cdot {\text{5m}}$
B) ${\text{0}} \cdot {\text{92m}}$
C) ${\text{1m}}$
D) ${\text{1}} \cdot {\text{84m}}$

Answer 1

Hint:The laws of reflection suggest that the reflected ray and the incident ray will lie on the same plane when incident light gets reflected from a plane mirror. The angle of incidence and the angle of reflection will be the same. These two statements imply that the point of incidence of the incident ray lies midway between the object and eye if the object and the eye were to lie on the same vertical line. Here, we consider the top of man’s head and his feet as two objects placed in front of the mirror.

Complete step by step answer.
Step 1: Sketch a figure of the man in front of the mirror looking at his image and list the parameters mentioned in the question.

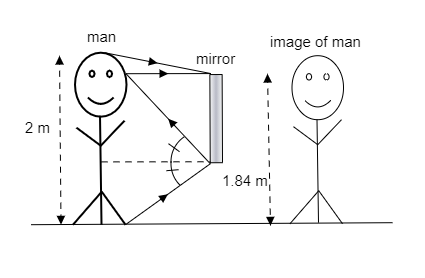
In the above figure, we see the man looking at his reflection in the mirror. The top of the man’s head and his feet are considered as two objects.
 The height of the man is mentioned as ${h_{o1}} = 2{\text{m}}$ . His eyes are located at a distance of ${s_{ground}} = 1 \cdot 84{\text{m}}$ from the ground i.e., they are at a distance of ${s_{head}} = 2 - 1 \cdot 84 = 0 \cdot 16{\text{m}}$ from the top of his head.
Step 2: Using the laws of reflection we can find the distance at which the upper edge and lower edge of the mirror lie.
According to the laws of reflection, for object 1 which is the top of the man’s head, the point of incidence of the ray from the object 1 will be midway between the location of his eyes and the object 1.
i.e., ${\text{upper edge}} = {h_{o1}} - \dfrac{{{s_{head}}}}{2}$ ------ (1)
Substituting for ${h_{o1}} = 2{\text{m}}$ and ${s_{head}} = 0 \cdot 16{\text{m}}$ in equation (1) we get, ${\text{upper edge}} = 2 - \dfrac{{0 \cdot 16}}{2} = 1 \cdot 92{\text{m}}$
Thus the upper edge of the mirror will be located at a distance of $1 \cdot 92{\text{m}}$ from the ground.
Similarly, for object 2 being the man’s feet, the point of incidence of the ray from object 2 will be midway between the location of his eyes and object 2.
i.e., ${\text{lower edge}} = \dfrac{{{s_{ground}}}}{2}$ ------ (2)
Substituting for ${s_{ground}} = 1 \cdot 84{\text{m}}$ in equation (2) we get, ${\text{lower edge}} = \dfrac{{1 \cdot 84}}{2} = 0 \cdot 92{\text{m}}$
Thus the lower edge of the mirror will be located at a distance of $0 \cdot 92{\text{m}}$ from the ground.
So the minimum vertical length of the mirror will be $1 \cdot 92 - 0 \cdot 92 = 1{\text{m}}$ .

Thus the correct option is C.

Note: As the man looks at his image in the mirror, the top of his head, his eyes and his feet lie in the same vertical line. So the point of incidence of the rays from the top of his head (or his feet) will be located at a distance which is half the distance between his eyes and the top of his head (or his feet). Thus the length of the mirror in the vertical direction must be at least half of the height of the man so that his whole reflection is seen in the mirror.