Question

A magnetic field $B = {B_0}j$ exists in the region $a < x < 2a$ and $B = - {B_0}j$ in the region 2a < x < 3a, where ${B_0}$ is a positive constant. A positive point charge moving with a velocity $v = {v_0}j,$ where ${v_0}$ is a positive constant, enters the magnetic field at $x = a$. The trajectory of the charge in this region can be like

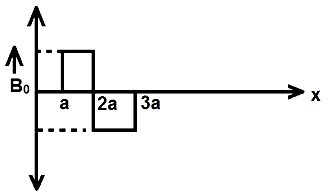
A.

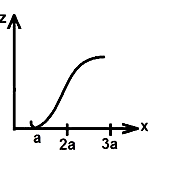
B.

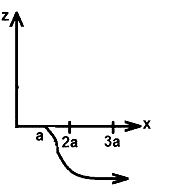
C.

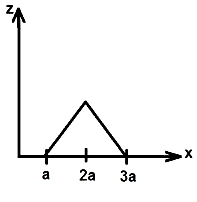
D.

Answer 1

Hint: Here, in this question, we need to find out the change in trajectory of the region when the point charge displaces its position. To find that, we need to first find the force experienced by the charge with the velocity and magnetic field. Then we need to also find the change in force experienced by the charge when the position of the charge is changed. In that way we can find the direction movement of point charge and can conclude with the path followed by it.

Complete answer:
Step one-
The region in which the magnetic field vector lies is given in the question.
First of all we need to find the force experienced by the magnetic field vector at each position.
We already know that, the force experienced by the charge $q$ is given by, $F = q(v \times B)$
Step two-
Using the above formula, we need to find the force experienced by the charge in the given regions.
Now, in the region, $x = a$ to $x = 2a,$ force experienced by the charge is
${F_1} = q({v_0}i \times {B_0}j)$…………..(i)
Now, we know that $i \times j = k$
Using this relation in equation (i), we get,
${F_1} = q{v_0}{B_0}k$
We know that $'k'$ denotes the z axis.
Therefore, ${F_1}$ is along the positive z axis.
Step three-
Similarly, we need to find the force experienced by the charge in the region, $x = 2a$ to $x = 3a$
So, ${F_2} = q({v_0}i \times - {B_0}j)$
$\therefore {F_2} = - q{v_0}{B_0}k$
As we know that $' - k'$ denotes the negative z axis.
Therefore, ${F_2}$ is in the negative z axis.
So we can conclude that ${F_1}$ and ${F_2}$ are perpendicular to the direction of velocity.
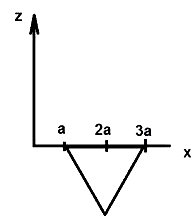
When we trace the path of trajectory, then we find that the graph given in option (A) is suited.

Hence, option (A), is the correct graph of the given question.

Note:
Magnetic fields exert forces on moving charges. The direction of the magnetic force on a moving charge is perpendicular to the plane formed by the velocity and magnetic field. The direction is given by right hand rule. The force experienced by a charge in a magnetic field is given by,$F = q(v \times B)$.