Question

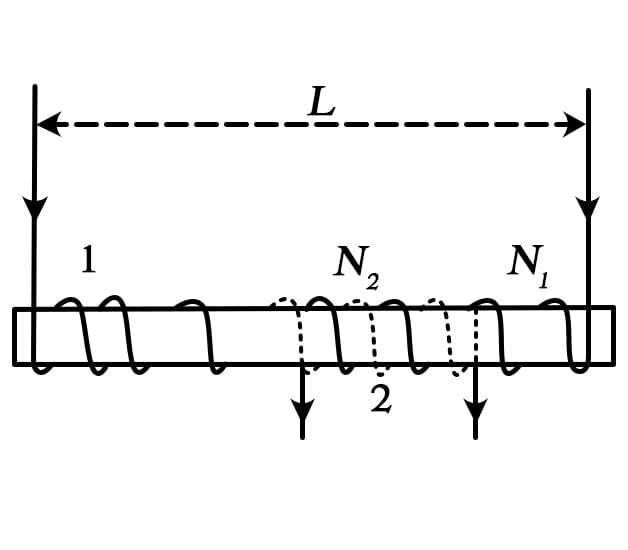
A long solenoid of length L, cross section A having ${N_1}$turns has wound about its center with a small coil of ${N_2}$ turns as shown in fig. The mutual inductance of two circuit is:

(a) $\dfrac{{{\mu _0}A({N_1}/{N_2})}}{L}$
(b) $\dfrac{{{\mu _0}A({N_1}{N_2})}}{L}$
(c) ${\mu _0}A{N_1}{N_2}L$
(d) $\dfrac{{{\mu _0}A({N_1}^2{N_2})}}{L}$

Answer 1

Hint:Since both solenoids have the same axis, therefore, the magnetic field of primary solenoid (source of magnetic field) gives flux to the secondary coil. Mutual inductance is a mutual property of a correlated system and linked to flux ($\phi $) through the other solenoid. The changing magnetic flux due to coil one induces a emf or current in coil two.


Formula Used:
1. Flux through the cross section of a coils of N turns is given by: $\phi = NB.A$ …… (1)
Where,
A=cross section area of the coil
N= total turns of the wire wound
B= Magnetic field through the coil
$\phi $= Total flux linked to the coil of N turns

2. Magnetic field produced due to a solenoid along its axial line is given by:
$B = \dfrac{{{\mu _0}NI}}{L}$ …… (2)
Where,
${\mu _0}$= Magnetic permeability of the space.
B= Magnetic field through the coil
N= total turns of the wire wound
I= total current through the wire
L= Length of the solenoid

3. Magnetic flux induced in coil/solenoid is also given in terms of mutual inductance by:
$\phi = MI$ …… (3)
Where,
$\phi $= Total flux linked to the coil of N turns
M= Mutual inductance with coil
I= Current through primary the coil.


Complete step by step answer:
${N_1}$: number of turns in primary solenoid
${N_2}$: number of turns in secondary solenoid
$\phi $= Total flux linked to the solenoid of ${N_2}$turns
Let I be current through primary solenoid

Step 1:
Using equation (1) we get magnetic field produced due to primary solenoid
$B = \dfrac{{{\mu _0}{N_1}I}}{L}$ …… (4)

Step 2:
Magnetic fields produced by primary solenoid will be a source of flux for secondary coils of ${N_2}$ turns.
Using equation (1) we get flux linked to secondary coil as $\phi = {N_1}B.A$
Substituting value from equation (4) we get,
$ \Rightarrow \phi = {N_2}\left( {\dfrac{{{\mu _0}{N_1}I}}{L}} \right)A$
Rearranging terms of above equation gives $ \Rightarrow \phi = \left( {\dfrac{{{\mu _0}{N_1}{N_2}A}}{L}} \right)I$ …… (5)

Step 3:
Comparing equation (5) with equation (3) we can say,$M = \left( {\dfrac{{{\mu _0}{N_1}{N_2}A}}{L}} \right)$ which is nothing but mutual inductance between two coils.

Final Answer
Hence, option (b) $\dfrac{{{\mu _0}{N_1}{N_2}A}}{L}$ is correct.

Note: One should note that the mutual inductance of a particular system is basically just dependent on the geometry of the system and the medium in which it is placed and it is independent of the current or changing magnetic field/flux.