Question

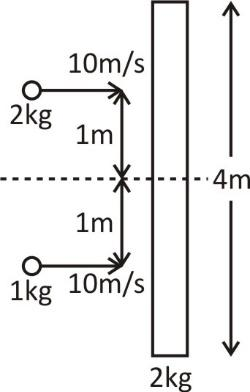
A long slender rod of mass $2\,kg$ and length $4\,m$ is placed on a smooth horizontal table. Two particles of masses $2\,kg$ and $1\,kg$ strike the rod simultaneously and stick to the rod after collision as shown in figure.If the two particles strike the rod in opposite direction then after collision, as compared to the previous situation the rod will

A. Rotate faster but translate at the same rate
B. Show no change in linear or angular velocity
C. Rotate slower and translate faster
D. Rotate faster and translate slower

Answer 1

Hint: Here we apply the law of conservation for both linear and angular momentum when the particles are on the same side and again when the particles are on the opposite side. And at last we have to compare the velocities of the linear and angular momentum in both the cases.

Complete step by step answer:
Mass of rod $m = 2\,kg$
Length of the rod $l = 4\,m$
Let ${m_1}$ be the mass of the first particle.
So, ${m_1} = 2\,kg$
Let ${m_2}$ be the mass of the first particle.
So, ${m_2} = 1\,kg$
Let ${v_1}$ be the velocity of the first particle.
So, ${v_1} = 10\,m/s$
Let ${v_2}$ be the velocity of the first particle.
Let ${v_c}$ be the velocity after collision.
Let ${R_1}$ be the distance between the first particle and the rod.
So, ${R_1} = 1\,m$
Let ${R_2}$ be the distance between the second particle and the rod.
So, ${R_2} = 1\,m$
Let ${m_c}$ be the mass after collision.
Therefore, ${m_c} = 2 + 1 + 2 = 5\,kg$
So, ${v_2} = 10\,m/s$
Here, the resultant force ${F_{net}}$ will be zero and linear momentum will be conserved.
${F_{net}} = 0$
Now, according to law of conservation of mass-
$
  {m_1}{v_1} + {m_2}{v_2} = {m_c}{v_c} \\
\implies 2 \times 10 + 1 \times 10 = 5 \times {v_c} \\
\implies {v_c} = 6\,m/s \\
$
Here resultant torque will also be zero. So, angular momentum will also be conserved
${\tau _{net}} = 0$
Let ${I_c}$ be the inertia of the rod after collision
Where
   $
  {I_c} = m\dfrac{{{l^2}}}
{{12}} + {m_1}{R_1}^2 + {m_2}{R_2}^2 \\
   = 2\dfrac{{{4^2}}}
{{12}} + 2 \times {1^2} + 1 \times {1^2} \\
$
And $\omega $ be angular momentum
According to law of conservation of momentum and putting the value of ${I_c}$ we get-
$
  {m_1}{v_1}{R_1} - {m_2}{v_2}{R_2} = {I_c}\omega \\
  2 \times 10 \times 1 - 1 \times 10 \times 1 = (2\dfrac{{{4^2}}}
\implies {{12}} + 2 + 1)\omega \\
\implies \omega = \dfrac{{30}}{{17}}rad/s \\
$
Now let us see what happens when the two particles strike the rod in opposite direction
Again taking linear momentum conserved-
If the two particles strike the rod in opposite direction then after collision then for angular momentum velocity becomes negative
${v_2} = - {v_2}$
Again,
$
  {m_1}{v_1} - {m_2}{v_2} = 5 \times {v_c}' \\
\implies 2 \times 10 - 10 \times 1 = 5{v_c}' \\
\implies {v_c}' = 2\,m/s \\
$
But we found that
${v_c} = 6\,m/s$
So, velocity decreases in this case
Hence, the rod will translate slower in this case.
Now, let us again see for angular momentum-
Applying law of conservation of momentum-
$
{m_1}{v_1}{R_1} - {m_2}( - {v_2}){R_2} = {I_c}\omega ' \\
\implies 2 \times 10 \times 1 + 1 \times 10 \times 1 = (2\dfrac{{{4^2}}}
 {{12}} + 2 + 1)\omega ' \\
\implies \omega ' = \dfrac{{90}}
{{17}}\,rad/s \\
$
But earlier we found that-
$\omega = \dfrac{{30}}
{{17}}\,rad/s$
So, the rod will rotate faster when the two particles strike the rod in opposite directions.

So, the correct answer is “Option D”.

Note:
Here we have to be careful while calculating the angular momentum when two particles strike the rod from opposite directions as the sign convention of velocity changes.
While solving this question we have one case ie-:If the two particles strike the rod in opposite directions then after collision then for angular momentum velocity becomes negative.