Question

A long conducting wire carrying a current 1 is bent at ${{120}^{o}}$(see figure). The magnetic field B at a point P on the right bisector of bending angle at a distance d from the bend is (${{\mu }_{0}}$ is the permeability of free space)

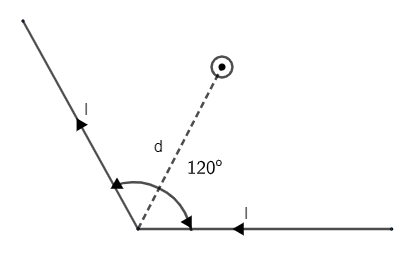
Answer 1

Hint: To measure the magnetic field at point P then first we have to take a single wire as two different from bend point then we have to measure perpendicular distance of point P from the both wire. Then by substituting this value in the magnetic field formula we can get the total magnetic field at point P.
Formula used:
$B=\dfrac{{{\mu }_{0}}I}{4\pi d}\left( \sin {{\theta }_{1}}+\sin {{\theta }_{2}} \right)$

Complete answer:
First we will draw a perpendicular line from the point P on the both parts of the wire as shown in the figure.

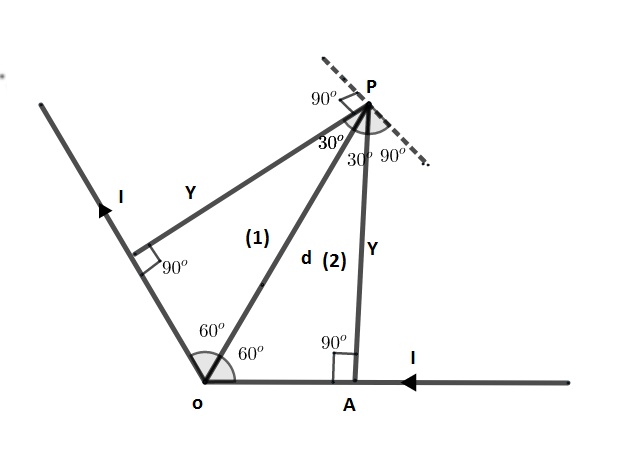
Consider now by using geometry of the triangle as shown in the figure.
As we can see that the angle of the both the triangles are the same, therefore both triangles will have same values of the side.
Therefore from the triangle OPA
$\sin {{60}^{o}}=\dfrac{Y}{d}$
Where, Y = perpendicular distance from the wire to the point P.
$Y=\dfrac{d\sqrt{3}}{2}...\left( 1 \right)$
Now formula for magnetic field,
$B=\dfrac{{{\mu }_{0}}I}{4\pi Y}$
Where,${{\mu }_{0}}$= permittivity of free space.
I = current flowing in the wire.
${{\theta }_{1}},{{\theta }_{2}}=$ angles a side of a perpendicular line.
For the triangle 1,
${{B}_{1}}=\dfrac{{{\mu }_{0}}I}{4\pi Y}\left( \sin {{30}^{o}}+\sin {{90}^{o}} \right).....\left( 2 \right)$
Substitute value of Y in the equation (2)
\[\begin{align}
& {{B}_{1}}=\dfrac{{{\mu }_{0}}I}{4\pi }\times \dfrac{2}{\sqrt{3}d}\left( \dfrac{1}{2}+1 \right) \\
& =\dfrac{{{\mu }_{0}}I}{4\pi d}\times \dfrac{2}{\sqrt{3}d}\left( \dfrac{3}{2} \right) \\
& {{B}_{1}}=\dfrac{\sqrt{3}{{\mu }_{0}}I}{4\pi d}....\left( 3 \right) \\
\end{align}\]
As we know that both the triangles are the same, so their magnetic field is also the same.
${{B}_{2}}=\dfrac{\sqrt{3}{{\mu }_{0}}I}{4\pi d}....\left( 4 \right)$
Now total magnetic field,
$B={{B}_{1}}+{{B}_{2}}....\left( 5 \right)$
Now substitute value of the equation (3) and (4) in the equation (5)
$\begin{align}
& B=\dfrac{\sqrt{3}{{\mu }_{0}}I}{4\pi d}+\dfrac{\sqrt{3}{{\mu }_{0}}I}{4\pi d} \\
& =2\times \dfrac{\sqrt{3}{{\mu }_{0}}I}{4\pi d} \\
& B=\dfrac{\sqrt{3}{{\mu }_{0}}I}{2\pi d} \\
\end{align}$
Therefore total magnetic field due to long conducting wire at point ‘P’ IS $\dfrac{\sqrt{3}{{\mu }_{0}}I}{2\pi d}$

Note:
As we know that both the triangles are same and at same perpendicular distance with the point ‘P’ so that we can directly multiply with ‘2’ in the equation of the magnetic field,
$B=2\times \dfrac{{{\mu }_{0}}I}{4\pi Y}\left( \sin {{\theta }_{1}}+\sin {{\theta }_{2}} \right)$
This will give an answer in a short step.