
A long capillary tube of mass $\pi$ gram, radius 2 mm and negligible thickness, is partially immersed in a liquid of surface tension 0.1 N/m. Take the angle of contact zero and neglect the buoyant force of the liquid. The force required to hold the tube vertically will be ($g= 10 m/s^2$):
$\text{A.}\quad 10.4 \pi mN$
$\text{B.}\quad 10.8 \pi mN$
$\text{C.}\quad 0.8 \pi mN$
$\text{D.}\quad 4.8 \pi mN$
Answer
587.1k+ views
Hint: When a capillary tube is immersed in liquid, due to the surface tension of the liquid, it applies some force on the interface of the tube. Due to this reason, liquid climbs some height in the capillary tube, called capillary rise. Hence some liquid will enter the tube and hence the net weight of the tube will increase.
Formula used: $F = Tl$
Complete step-by-step solution:
Here we are supposed to find the force that must be applied on the tube to hold it vertically. Now, we’ll see what surface tension is. Surface tension: It is the property of liquid by the virtue of which the surface of the liquid acts as a stretched membrane. In other words, the surface wants to minimize its area, and hence when a body is immersed in a liquid, the liquid exerts a force on the touching boundary of the liquid and the body. Hence the net force must be equal to the weight of the tube and water rose in the tube, for equilibrium, as shown in the figure.
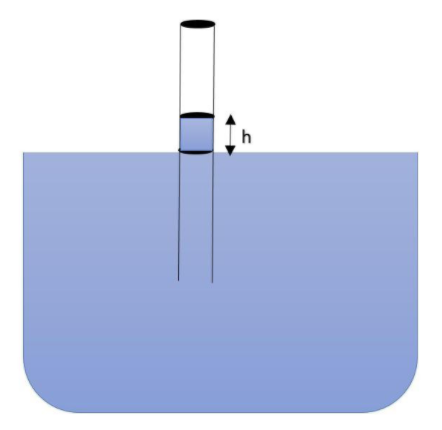
But we can find the weight of water rose directly by knowing the force exerted by the liquid on the interface.
The force is given by $F = Tl$ where ‘l’ is the length of the interface.
Here $l = 2\pi r$
Hence $F = 2T\pi r$
But note that, there are two interfaces, one on the top of the water rose and the other on the surface of the water in the beaker.
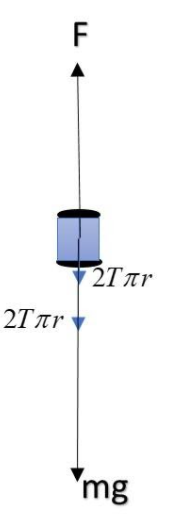
Thus, total force(F) that is needed to be applied = weight of tube + $4T\pi r$
$F = \pi\times 10^{-3} g + 4 (0.1)\pi (0.002) = (10 \pi + 0.8\pi )\times 10^{-3} = 10.8\pi \ mN$
Thus, option A. is correct.
Note: We have to take all the contact surfaces where the object and liquid have an interface. We can also calculate the height of the water column by equating the weight of water rose with $2\pi Tr$ because in that case, we’ll have only one interface, the upper surface since at the lower surface, the availability of water is continuous.
Formula used: $F = Tl$
Complete step-by-step solution:
Here we are supposed to find the force that must be applied on the tube to hold it vertically. Now, we’ll see what surface tension is. Surface tension: It is the property of liquid by the virtue of which the surface of the liquid acts as a stretched membrane. In other words, the surface wants to minimize its area, and hence when a body is immersed in a liquid, the liquid exerts a force on the touching boundary of the liquid and the body. Hence the net force must be equal to the weight of the tube and water rose in the tube, for equilibrium, as shown in the figure.

But we can find the weight of water rose directly by knowing the force exerted by the liquid on the interface.
The force is given by $F = Tl$ where ‘l’ is the length of the interface.
Here $l = 2\pi r$
Hence $F = 2T\pi r$
But note that, there are two interfaces, one on the top of the water rose and the other on the surface of the water in the beaker.

Thus, total force(F) that is needed to be applied = weight of tube + $4T\pi r$
$F = \pi\times 10^{-3} g + 4 (0.1)\pi (0.002) = (10 \pi + 0.8\pi )\times 10^{-3} = 10.8\pi \ mN$
Thus, option A. is correct.
Note: We have to take all the contact surfaces where the object and liquid have an interface. We can also calculate the height of the water column by equating the weight of water rose with $2\pi Tr$ because in that case, we’ll have only one interface, the upper surface since at the lower surface, the availability of water is continuous.
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Difference Between Plant Cell and Animal Cell

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Who is eligible for RTE class 9 social science CBSE

Which places in India experience sunrise first and class 9 social science CBSE

What is pollution? How many types of pollution? Define it

Name 10 Living and Non living things class 9 biology CBSE




