Question

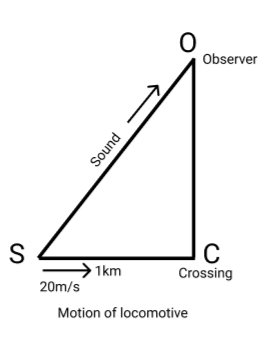
A locomotive approaching a crossing at a speed of \[20m/s\] around a whistle of frequency $640Hz$ when $1km$ from crossing. There is no wind and the speed of around air is $330m/s$ . What frequency is heard by an observer $\sqrt 3 km$ on the straight road from crossing at a right angle?

$\left( a \right){\text{ }}600Hz$
$\left( b \right){\text{ }}660Hz$
$\left( c \right){\text{ }}630Hz$
$\left( d \right){\text{ }}720Hz$

Answer 1

Hint: So in this question, we have to find the velocity which will be in the direction of the observer from the source point. For this, first of all, we will calculate the velocity by using the base and hypotenuse, and then by applying the Doppler’s effect which is $\mu ' = \dfrac{{\mu \times v}}{{\left( {v - {v^ \circ }} \right)}}$ , we will get the final frequency.
Formula used:
$\cos \theta = \dfrac{B}{H}$
Here,
$B$ , will be the base
And $H$ , will be the hypotenuse
Doppler’s effect,
$\mu ' = \dfrac{{\mu \times v}}{{\left( {v - {v^ \circ }} \right)}}$
Here,
$\mu '$ , will be the final frequency
$\mu $ , will be the initial frequency
${v^ \circ }$ , will be the velocity
$v$, will be the speed

Complete Step By Step Solution As we know from the figure and question, we can see there is the right triangle made so firstly we will calculate the velocity.
So for this, we know
$\cos \theta = \dfrac{B}{H}$
Therefore, the velocity will be
$v\cos \theta $
Now on substituting the values we get,
$Velocity = 20m/s \times \dfrac{1}{2}$
On solving the above equation, we get
$ \Rightarrow v = 10m/s$
Now we will apply the Doppler’s effect
As we know the formula
$\mu ' = \dfrac{{\mu \times v}}{{\left( {v - {v^ \circ }} \right)}}$
Now substituting the values we get
Again solving it, we get
$ \Rightarrow \mu ' = 640 \times 330/\left( {320} \right)Hz$
So on solving the last equation, we will get
$ \Rightarrow \mu ' = 660Hz$
Therefore, $660Hz$ will be the final frequency.

Hence, the option $B$ will be correct.

Note: The Doppler Effect is an impact seen in light and sound waves as they advance toward or away from a spectator. One basic cause of the Doppler impact is the sound of a car horn. Picture an individual remaining on a city intersection. A vehicle draws near, blowing its horn. As the vehicle keeps advancing toward the individual, the pitch of the horn seems to expand; its sound goes increasingly elevated. As the vehicle passes the onlooker, notwithstanding, the impact is turned around. The pitch of the vehicle horn becomes lower and lower.