Question

A load W is suspended from a self-propelled crane by a cable of length ‘d’. The crane and load are moving at a constant speed ${{v}_{0}}$ . The crane is stopped by the bumper and loads on the cable swings. Given that the angle of swing is ${{60}^{0}}$ and $d=5m.$ If the initial velocity of the crane is ${{v}_{0}}m{{s}^{-1}}$, find ${{v}_{0}}$ .
       

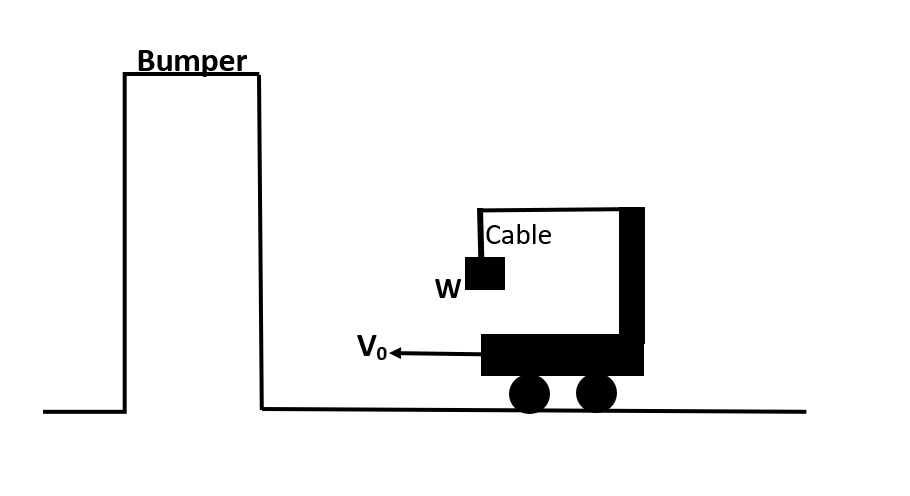
Answer 1

Hint: Since the crane is stopped by the bumper, the load will start to oscillate. We have been given the angle of swing. We can use it to calculate the change in height of the load. Now, on applying conservation of energy for the load, we can say that its initial kinetic energy is equal to the energy gained by the load at its maximum height of oscillation (because at this point it’s velocity will be zero). We shall use this to solve our problem.

Complete answer:
Let us see the swinging motion of crane with the help of following diagram:
     

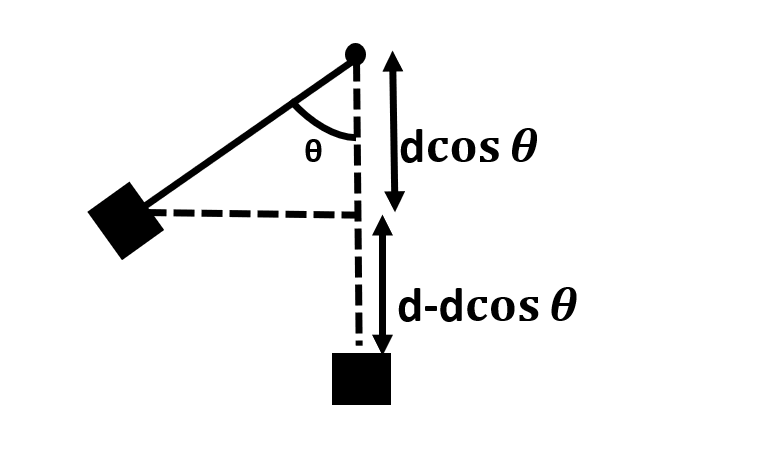
Let the length of the cable be ‘d’.
Then, the gain in height (say h) could be given by:
$\Rightarrow h=d-d\cos \theta $
Where, the value of angle of swing is given to us as:
$\Rightarrow \theta ={{60}^{0}}$
Also, since the load was attached to the crane, its initial velocity is the same as the velocity of the crane.
And its velocity at the highest point of swing is equal to zero because all the kinetic energy has been converted to gravitational potential energy.
Thus, applying conservation of energy for the load, we can write:
$\begin{align}
  & \Rightarrow \dfrac{1}{2}\left( \dfrac{W}{g} \right){{v}_{o}}^{2}+0=W(d-d\cos {{60}^{0}}) \\
 & \Rightarrow {{v}_{o}}^{2}=2gd(1-\cos {{60}^{0}}) \\
 & \Rightarrow {{v}_{o}}=\sqrt{2gd(1-\cos {{60}^{0}})} \\
\end{align}$
Thus, putting the value of all the known terms and simplifying, we get:
$\begin{align}
  & \Rightarrow {{v}_{0}}=\sqrt{2\times 9.8\times 5\left( 1-\dfrac{1}{2} \right)} \\
 & \Rightarrow {{v}_{0}}=\sqrt{49}m{{s}^{-1}} \\
 & \therefore {{v}_{0}}=7m{{s}^{-1}} \\
\end{align}$
Hence, the initial velocity of the crane comes out to be 7 meters per second.

Note:
We should be able to visualize the elements in question on which we could apply the conservation of energy. We applied the conservation of energy on the load because there is no external force acting on it that could hamper our equation for conservation of energy. Also, in lengthy calculations like these, one should always revise their solutions.