Question

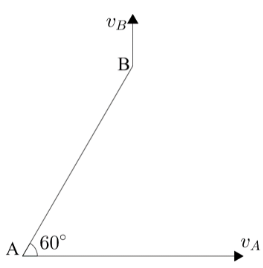
A link $\;AB$ is moving in a vertical plane. At a certain instant when the link is inclined $60^{\circ}$ to the horizontal, the point $A$ is moving horizontally at $3ms^{-1}$ , while $B$ is moving in the vertical direction. What is the velocity of $B$ ?

A. $\dfrac{1}{\sqrt{3}}m{{s}^{-1}}$
B. $2\sqrt{3}m{{s}^{-1}}$
C. $\sqrt{3}m{{s}^{-1}}$
D. $\dfrac{\sqrt{3}}{2}m{{s}^{-1}}$

Answer 1

Hint: Here, we are given the velocities of both the ends of the link. We know that the link is rigid, and hence the length of the link will be fixed. Thus the resultant velocity of both the components along the link will be the same. Hence, from the given velocity, we can find the velocity along the link and from that, we can find the velocity of the required component.

Complete step by step answer:
Here, we are given a rigid link, whose length remains constant. The link is moving at $60^ \circ$ with the horizontal, with both the ends having velocity of different magnitude and directions. Here, we are given the velocity of the point $A$ as $v_A=3ms^{-1}$.

Now, this is the velocity of the point itself. We can find the velocity of the point along the link $\;AB$ by considering the component of the velocity in the direction of the link as shown in figure.

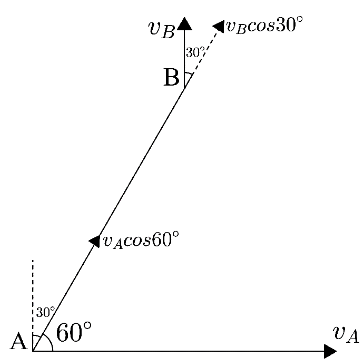
Hence, the velocity of the point $A$ along the link as shown in the figure is given as
$v'={{v}_{A}}\cos 60{}^\circ $
Substituting the values,
$\therefore v'=\dfrac{3}{2}m{{s}^{-1}}$…… $(1)$
Now, as the link is rigid, the velocity of the point $B$ along the link $\;AB$ will be equal to the velocity of the point $A$ along the link.
From the above figure, the velocity of point $B$ along the link is given as
$v'={{v}_{B}}\cos 30{}^\circ $…… $(2)$
Equating both the equations,
$\therefore \dfrac{3}{2}={{v}_{B}}\times \dfrac{\sqrt{3}}{2}$
$\therefore {{v}_{B}}=\sqrt{3}m{{s}^{-1}}$

Hence, the correct answer is option C.

Note: We can also solve the given question, by assuming links for the given velocities. We know that the velocity is always perpendicular to the link. Hence, we can draw the links for the given velocities, we can draw the links as shown below,

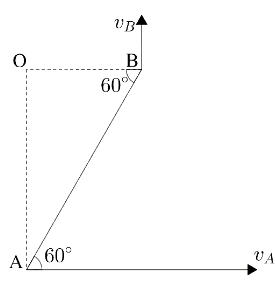
From the figure, we can find the ratio of the links $\cot 60{}^\circ =\dfrac{OB}{OA}$ . Now, we know that $\dfrac{OB}{OA}=\dfrac{{{v}_{B}}}{{{v}_{A}}}$
Hence, we can get the formula as ${{v}_{B}}=\cot 60{}^\circ \times {{v}_{A}}$
$\therefore {{v}_{B}}=\sqrt{3}m{{s}^{-1}}$