Question

A line which intersects a circle in only one point is called ___________ .

Answer 1

Hint: A tangent to a circle is a line that intersects the circle in exactly one point.
The word tangent originated from the Latin word \[TANGERE\] which means ‘to touch’.
To understand the existence of the tangent to a circle at a point let us perform the activities.

Complete step-by-step answer:
Activity 1:
Draw a circle and a secant \[AB\] of the circle. Now, draw various lines parallel to the secant \[AB\] on both sides of it.
      

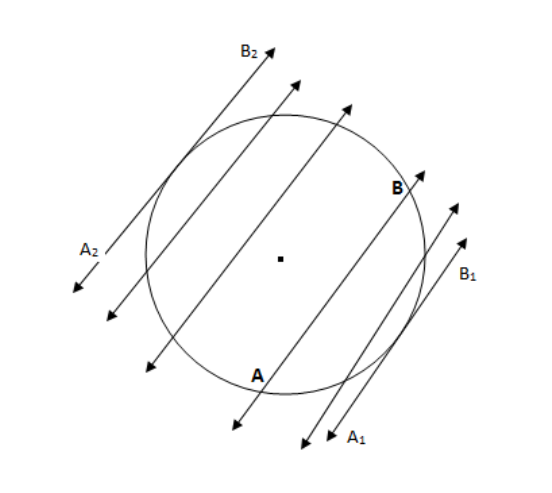
You can see that the lengths of chords cut by the lines decreases as we go away from the secant \[AB\] in the above figure. You will also notice that on the two sides of the secant \[AB\] , \[{{A}_{1}}{{B}_{1}}\] and \[{{A}_{2}}{{B}_{2}}\] are the limiting positions of secants when the lengths of the chords cut become zero. These are the tangents to the circle parallel to the secant \[AB\] .
So, from the activity we can conclude that there cannot be more than two tangents parallel to the given secant.
Activity 2:
Take a circular wire and a straight wire \[AB\] . Attach the straight wire \[AB\] at the point \[P\] of the circular wire in such a way that \[AB\] can rotate about the point \[P\] in a plane. Put the system on the table and rotate wire \[AB\] about the point \[P\] to get different positions of the wire.

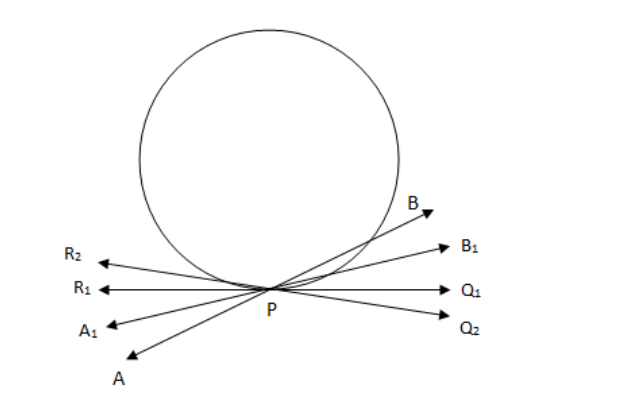
You can see that wire \[AB\] intersects the circular wire at \[P\] and at another point \[{{Q}_{1}}\] or \[{{Q}_{2}}\] etc. when it is rotated clockwise. When it is rotated anticlockwise it will intersect at \[{{R}_{1}}\] or \[{{R}_{2}}\] .
This activity shows that the tangent at a point to a circle is the limiting position of the secant.
Therefore, a line which intersects a circle in only one point is called a tangent to the circle.

Note: The point of contact is the only point which is common to the tangent and the circle and every other point on the tangent lies outside the circle. So, of all points on a tangent to a circle the point of contact is nearest to the centre of the circle.