Question

A line segment l of length a cm is rotated about a vertical line L, keeping the line l in one of the following three poison
i.l is parallel to L and at a distance of r cm. from L,
ii.l is perpendicular to L and its mid-point is at a distance r cm, from L,
iii.l and L are in the same plane and is inclined to L an angle with it mid-point at a distance r cm from L.
Let \[{A_1},{A_2},{A_3}\]be the area so generated. If \[r > \left( {\dfrac{a}{2}} \right)\], then
A. \[{A_1} < {A_3} < {A_2}\]
B .\[{A_1} = {A_3} < {A_2}\]
C. \[{A_2} < {A_1} < {A_3}\]
D. \[{A_1} = {A_2} = {A_3}\]

Answer 1

Hint: A part of a line that has two endpoints and the shortest distance between them, is a line segment. To find, the condition if \[r > \left( {\dfrac{a}{2}} \right)\], then we need to find the value of \[{A_1},{A_2},{A_3}\]in which we need to construct the diagrams according to the given statements (I, II, III). Hence based on this we have the values of \[{A_1},{A_2},{A_3}\]if \[r > \left( {\dfrac{a}{2}} \right)\].

Complete step by step solution:
Let us write the given data:
A line segment l of length a cm i.e.,
\[l = \left( a \right)cm\]
Given,
In case I we have: A line segment l is parallel to vertical line L and at a distance of r cm. from L, hence we get:
\[{A_1} = 2\pi ra\]

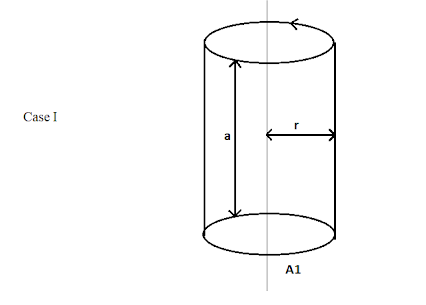
In case II we have: A line segment l is perpendicular to vertical line L and its mid-point is at a distance r cm, from L as:

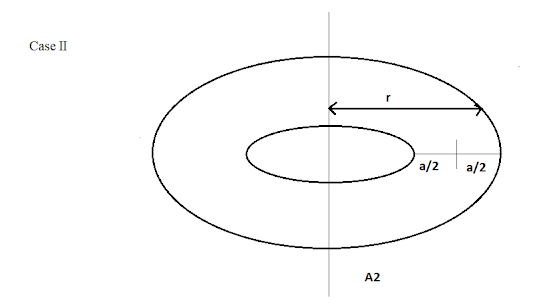
\[{A_2} = \pi {\left( {r + \dfrac{a}{2}} \right)^2} - \pi {\left( {r - \dfrac{a}{2}} \right)^2}\]
Here, line segment l is perpendicular to L and its mid-point is at a distance r cm, from L, hence we get:
\[ \Rightarrow {A_2} = 2\pi ra\]
In case III we have: A line segment l and vertical line L are in the same plane and is inclined to L an angle with it mid-point at a distance r cm from L as:

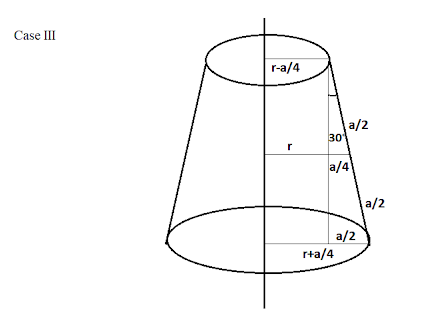
Here,
\[{A_3} = \pi a\left( {r - \dfrac{a}{4} + r + \dfrac{a}{4}} \right)\]
As l and length L are in the same plane and is inclined to L an angle with it mid-point at a distance r cm from L, hence we get:
\[ \Rightarrow {A_3} = 2\pi ra\]
Hence, we have \[{A_1} = {A_2} = {A_3}\].


Note: We must note that a line segment has endpoints whereas a line extends infinitely at both ends i.e., a line has no endpoints and extends infinitely in both the direction but a line segment has two fixed or definite endpoints. Hence, based on the given statements of line segment l of length a cm and vertical line L; we need to find the value of \[{A_1},{A_2},{A_3}\].