Question

A line segment has endpoints at \[\left( {1,4} \right)\] and $\left( {4,9} \right)$. The line segment is dilated by a factor of $\dfrac{1}{3}$ around $\left( {4,2} \right)$. What are the new endpoints and length of the line segment?

Answer 1

Hint: Here, in the given question we are given, a line segment has endpoints at \[\left( {1,4} \right)\] and $\left( {4,9} \right)$ and this line segment is dilated by a factor of $\dfrac{1}{3}$ around $\left( {4,2} \right)$ and we need to find the new points and length of the line segment. Dilation is a transformation, which is used to resize the object. Dilation is used to make the objects larger or smaller. At first we will find the new endpoints using the dilution factor. If a point $A$ of coordinate $\left( {a,b} \right)$ be dilated by a factor $n$ around the point of coordinate $\left( {h,k} \right)$, then after dilation the new position will be $A' = \left( {n\left( {a - h} \right) + h,n\left( {b - k} \right) + k} \right)$. After this, we will find the length of line segment of new end points using distance formula, $D = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} $.

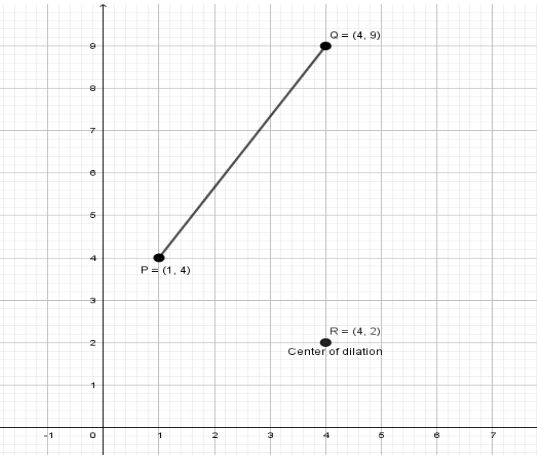
Let $\overline {PQ} $ be a line segment on the coordinate plane with endpoints at \[\left( {1,4} \right)\] and $\left( {4,9} \right)$. The absolute value of the scale factor $\left( n \right)$, with the constraint $0 < n < 1$, reduces the line segment $\overline {PQ} $, enlarges if otherwise. Scale factor of dilation is $\dfrac{1}{3}$. Now, let us find the new endpoints using $\left( {n\left( {a - h} \right) + h,n\left( {b - k} \right) + k} \right)$. Given, endpoints \[P\left( {1,4} \right)\] and $Q\left( {4,9} \right)$. For point \[P\left( {1,4} \right)\], we have $n = \dfrac{1}{3}$ and $\left( {h,k} \right) = \left( {4,2} \right)$. So, new endpoint will be:
$ \Rightarrow P' = \left( {\dfrac{1}{3}\left( {1 - 4} \right) + 4,\dfrac{1}{3}\left( {4 - 2} \right) + 2} \right)$

On subtraction of terms, we get
$ \Rightarrow P' = \left( {\dfrac{1}{3}\left( { - 3} \right) + 4,\dfrac{1}{3}\left( 2 \right) + 2} \right)$
On multiplication of terms, we get
$ \Rightarrow P' = \left( { - 1 + 4,\dfrac{2}{3} + 2} \right)$
Take LCM
$ \Rightarrow P' = \left( {3,\dfrac{{2 + 6}}{3}} \right)$
$ \Rightarrow P' = \left( {3,\dfrac{8}{3}} \right)$
For point \[Q\left( {4,9} \right)\], we have $n = \dfrac{1}{3}$ and $\left( {h,k} \right) = \left( {4,2} \right)$. So, new endpoint will be:
\[ \Rightarrow Q' = \left( {\dfrac{1}{3}\left( {4 - 4} \right) + 4,\dfrac{1}{3}\left( {9 - 2} \right) + 2} \right)\]

On subtraction of terms, we get
\[ \Rightarrow Q' = \left( {\dfrac{1}{3}\left( 0 \right) + 4,\dfrac{1}{3}\left( 7 \right) + 2} \right)\]
On multiplication of terms, we get
\[ \Rightarrow Q' = \left( {4,\dfrac{7}{3} + 2} \right)\]
Take LCM
\[ \Rightarrow Q' = \left( {4,\dfrac{{7 + 6}}{3}} \right)\]
$ \Rightarrow Q' = \left( {4,\dfrac{{13}}{3}} \right)$
New end-points: $P'\left( {3,\dfrac{8}{3}} \right)$ and $Q'\left( {4,\dfrac{{13}}{3}} \right)$.
We will plot these points on the graph as: $P'\left( {3,2.67} \right)$ and $Q'\left( {4,4.33} \right)$.

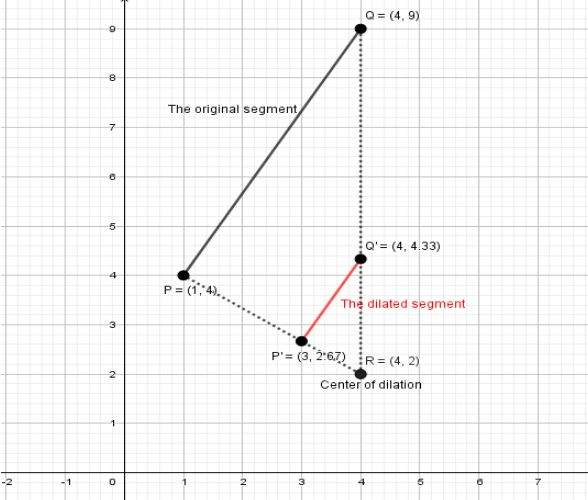
Here $\overline {PQ} $ is the preimage and after dilation, $\overline {P'Q'} $ is called the image. Note that the preimage and the image are parallel. Also as you can see after dilation the size of the pre-image is reduced. Observe that the points (center of dilation $R$, $P$ and $P'$) are collinear. And, the points (center of dilation $R$, $Q$ and $Q'$) are collinear.$\overline {PQ} \parallel \overline {P'Q'} $, since we have congruent corresponding angles.

Now, we will find the length of the line segment or length of the image $\overline {P'Q'} $.
Distance formula: $D = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} $, let $\left( {{x_1},{y_1}} \right)$ be $\left( {3,\dfrac{8}{3}} \right)$ and $\left( {{x_2},{y_2}} \right)$ be $\left( {4,\dfrac{{13}}{3}} \right)$. Therefore, on substituting the values, we get
$ \Rightarrow D = \sqrt {{{\left( {4 - 3} \right)}^2} + {{\left( {\dfrac{{13}}{3} - \dfrac{8}{3}} \right)}^2}} $
Take LCM
$ \Rightarrow D = \sqrt {{{\left( {4 - 3} \right)}^2} + {{\left( {\dfrac{{13 - 8}}{3}} \right)}^2}} $
On subtraction of terms, we get
$ \Rightarrow D = \sqrt {{{\left( 1 \right)}^2} + {{\left( {\dfrac{5}{3}} \right)}^2}} $
$ \Rightarrow D = \sqrt {1 + \dfrac{{25}}{9}} $

Take LCM
$ \Rightarrow D = \sqrt {\dfrac{{9 + 25}}{9}} $
On addition of terms, we get
$ \Rightarrow D = \sqrt {\dfrac{{34}}{9}} = \dfrac{{\sqrt {34} }}{{\sqrt 9 }}$
On substituting the value of $\sqrt 9 = 3$, we get
$ \Rightarrow D = \dfrac{{\sqrt {34} }}{3}$
Now we will substitute the value of $\sqrt {34} = 5.831$.
$ \Rightarrow D = \dfrac{{5.831}}{3}$
On division, we get
$ \therefore D = 1.94\,units$
Thus, length of line segment $\overline {P'Q'} = 1.94\,units$.

Therefore, the new endpoints are $P'\left( {3,\dfrac{8}{3}} \right)$ and $Q'\left( {4,\dfrac{{13}}{3}} \right)$ and length of line segment is $1.94\,units$.

Complete step by step answer:

Note: Remember that dilation is not an isometry. It creates similar figures only and dilation preserves the angle of measure. Remember that a scale factor of $n = 1$ means that the segment and its image are equal. The dilation does not enlarge or shrink the image of the figure; it remains unchanged. Also, when the scale factor $n > 1$, a dilation is an enlargement. When $0 < n < 1$, a dilation is a reduction.