Question

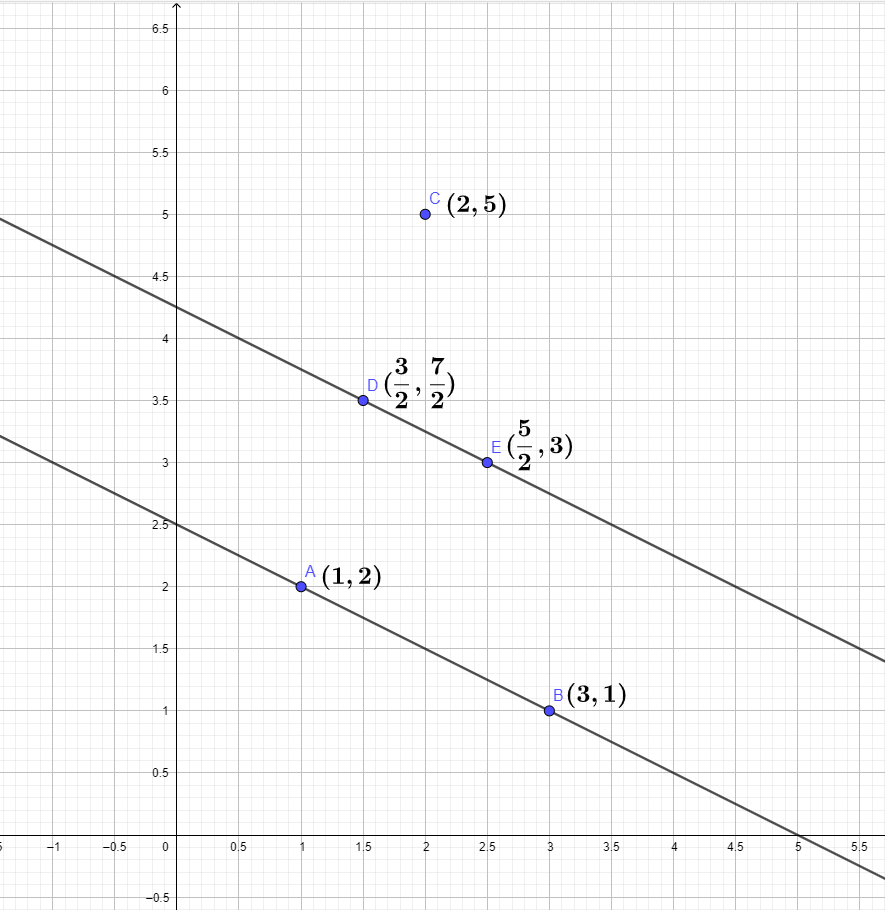
A line segment has endpoints at \[\left( {1,2} \right)\] and \[\left( {3,1} \right)\] . The line segment is dilated by a factor of \[\dfrac{1}{2}\] around \[\left( {2,5} \right)\] .What are the new endpoints and length of the line segment?

Answer 1

Hint: In order to solve this question, we will use the concept that if a point \[X\] of coordinate \[\left( {a,b} \right)\] is dilated by a factor \[n\] around the point of coordinate \[\left( {h,k} \right)\] , then after dilation the new position of point will be \[{X'} = \left( {n\left( {a - h} \right) + h,{\text{ }}n\left( {b - k} \right) + k} \right)\] .Firstly we will let \[A\] and \[B\] be the two endpoints of the line segment. After that we will let \[{A'}\] and \[{B'}\] be the new endpoints of the line segment after dilation and find them by substituting the values in the above formula. And finally, we will find the length of the dilated line segment using distance formula i.e., \[d = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \] .And hence we will get the required result.

Complete answer::
Let \[A\] and \[B\] be the two endpoints of the line segment.
which means \[A\left( {1,2} \right)\] and \[B\left( {3,1} \right)\] be the two endpoints of the line segment.
And let \[{A'}\] and \[{B'}\] be the two new endpoints of the line segment.
Now we know that
If a point \[X\] of coordinate \[\left( {a,b} \right)\] is dilated by a factor \[n\] around the point of coordinate, \[\left( {h,k} \right)\] then after dilation the new position of point will be
\[{X'} = \left( {n\left( {a - h} \right) + h,{\text{ }}n\left( {b - k} \right) + k} \right)\]
This means
\[X\left( {a,b} \right) = \xrightarrow{{dilated{\text{ }}nX{\text{ }}around{\text{ }}\left( {h,k} \right)}}{X'}\left( {n\left( {a - h} \right) + h,n\left( {b - k} \right) + k} \right)\]
Now it is given that
line segment is dilated by a factor of \[\dfrac{1}{2}\] around \[\left( {2,5} \right)\]
which means \[n = \dfrac{1}{2}\] and \[\left( {h,k} \right) = \left( {2,5} \right)\]
Using the formula, we get
\[A\left( {1,2} \right) = \xrightarrow{{dilated{\text{ }}\dfrac{1}{2}X{\text{ }}around{\text{ }}\left( {2,5} \right)}}{A'}\left( {\dfrac{1}{2}\left( {1 - 2} \right) + 2,{\text{ }}\dfrac{1}{2}\left( {2 - 5} \right) + 5} \right)\]
\[ \Rightarrow A\left( {1,2} \right) = \xrightarrow{{dilated{\text{ }}\dfrac{1}{2}X{\text{ }}around{\text{ }}\left( {2,5} \right)}}{A'}\left( {\dfrac{{ - 1}}{2} + 2,{\text{ }}\dfrac{{ - 3}}{2} + 5} \right)\]
On simplification, we get
\[A\left( {1,2} \right) = \xrightarrow{{dilated{\text{ }}\dfrac{1}{2}X{\text{ }}around{\text{ }}\left( {2,5} \right)}}{A'}\left( {\dfrac{3}{2},\dfrac{7}{2}} \right)\]
which means the first new endpoint is \[{A'}\left( {\dfrac{3}{2},\dfrac{7}{2}} \right)\]
Similarly,
\[B\left( {3,1} \right) = \xrightarrow{{dilated{\text{ }}\dfrac{1}{2}X{\text{ }}around{\text{ }}\left( {2,5} \right)}}{B'}\left( {\dfrac{1}{2}\left( {3 - 2} \right) + 2,{\text{ }}\dfrac{1}{2}\left( {1 - 5} \right) + 5} \right)\]
\[ \Rightarrow B\left( {3,1} \right) = \xrightarrow{{dilated{\text{ }}\dfrac{1}{2}X{\text{ }}around{\text{ }}\left( {2,5} \right)}}{B'}\left( {\dfrac{1}{2} + 2,{\text{ }}\dfrac{{ - 4}}{2} + 5} \right)\]
On simplification, we get
\[B\left( {3,1} \right) = \xrightarrow{{dilated{\text{ }}\dfrac{1}{2}X{\text{ }}around{\text{ }}\left( {2,5} \right)}}{B'}\left( {\dfrac{5}{2},3} \right)\]
which means the second new endpoint is \[{B'}\left( {\dfrac{5}{2},3} \right)\]
Therefore, the new endpoints are \[{A'}\left( {\dfrac{3}{2},\dfrac{7}{2}} \right)\] and \[{B'}\left( {\dfrac{5}{2},3} \right)\]
Now we know that
Distance formula, \[d = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \]
Therefore, the length of the dilated line segment will be
\[{A'}{B'} = \sqrt {{{\left( {\dfrac{5}{2} - \dfrac{3}{2}} \right)}^2} + {{\left( {3 - \dfrac{7}{2}} \right)}^2}} \]
\[ \Rightarrow {A'}{B'} = \sqrt {{{\left( 1 \right)}^2} + {{\left( {\dfrac{{ - 1}}{2}} \right)}^2}} \]
\[ \Rightarrow {A'}{B'} = \sqrt {\dfrac{5}{4}} \]
We know that \[\sqrt {\dfrac{a}{b}} = \dfrac{{\sqrt a }}{{\sqrt b }}\]

Therefore, we have
\[ \Rightarrow {A'}{B'} = \sqrt {\dfrac{5}{4}} = \dfrac{{\sqrt 5 }}{2}\]
We know that \[\sqrt 5 = 2.236\]
\[ \Rightarrow {A'}{B'} = \dfrac{{2.236}}{2} = 1.118\]
Hence, the new endpoints are \[{A'}\left( {\dfrac{3}{2},\dfrac{7}{2}} \right)\] and \[{B'}\left( {\dfrac{5}{2},3} \right)\]
and the length of line segment \[{A'}{B'} = 1.118\]

Note:
Alternative way to solve this problem is:
If \[{x_0}\] is the dilation centre, \[{x_1}\] and \[{x_2}\] are the coordinates of the endpoints of the line segment and \[\lambda \] is the factor of dilation, then the position of new endpoints will be given by:
\[x_1' = {x_0} + \lambda \left( {{x_1} - {x_0}} \right)\] and \[x_2' = {x_0} + \lambda \left( {{x_2} - {x_0}} \right)\]
So, here \[{x_0} = \left( {2,5} \right),{\text{ }}{x_1} = \left( {1,2} \right),{\text{ }}{x_2} = \left( {3,1} \right),{\text{ }}\lambda = \dfrac{1}{2}\]
Therefore, we get
\[x_1' = \left( {2,5} \right) + \dfrac{1}{2}\left( {\left( {1,2} \right) - \left( {2,5} \right)} \right)\]
\[ \Rightarrow x_1' = \left( {2,5} \right) + \dfrac{1}{2}\left( {1 - 2,2 - 5} \right)\]
\[ \Rightarrow x_1' = \left( {2,5} \right) + \left( {\dfrac{{ - 1}}{2},\dfrac{{ - 3}}{2}} \right)\]
\[ \Rightarrow x_1' = \left( {\dfrac{3}{2},\dfrac{7}{2}} \right)\]
And
\[x_2' = \left( {2,5} \right) + \dfrac{1}{2}\left( {\left( {3,1} \right) - \left( {2,5} \right)} \right)\]
\[ \Rightarrow x_2' = \left( {2,5} \right) + \dfrac{1}{2}\left( {3 - 2,{\text{ 1}} - 5} \right)\]
\[ \Rightarrow x_2' = \left( {2,5} \right) + \left( {\dfrac{1}{2}, - 2} \right) = \left( {\dfrac{5}{2},{\text{ }}3} \right)\]
Hence, the new endpoints are \[x_1' = \left( {\dfrac{3}{2},\dfrac{7}{2}} \right)\] and \[x_2' = \left( {\dfrac{5}{2},3} \right)\]
Now, the length of the dilated line segment will be
\[x_1'x_2' = \sqrt {{{\left( {\dfrac{5}{2} - \dfrac{3}{2}} \right)}^2} + {{\left( {3 - \dfrac{7}{2}} \right)}^2}} \]
\[ \Rightarrow x_1'x_2' = \dfrac{{\sqrt 5 }}{2} = \dfrac{{2.236}}{2}\]
\[ \Rightarrow x_1'x_2' = 1.118\]
Hence, the length of the line segment \[x_1'x_2' = 1.118\]
Hence, we get the required results.