Question

A line L: y = mx + 3 meets y-axis at E (0, 3) and the arc of the parabola ${{y}^{2}}=16x$ , $0\le y\le 6$ at the point F $({{x}_{0}},{{y}_{0}})$ .The tangent to the parabola at F $({{x}_{0}},{{y}_{0}})$ intersects the y-axis at G $(0,{{y}_{1}})$ .The slope m of the line L is chosen such that the area of $\Delta $ EFG has a local maximum.
Match List I and List II and select the correct answers using the code given below the lists.

List I	List II
m =	1. 1/2
	2. 4
	3. 2
	4. 1

Answer 1

Hint: To solve the above problem, we will use the concept of parametric equation of parabola which is of the form $x=a{{t}^{2}},y=2at$, here a = 4. Then taking point F as the parametric point of the parabola we get the equation of the tangent at that point. After that we find its y-intercept and get the coordinate G, then using the formula to find the area of the triangle we get the area of triangle EFG in terms of t. After that differentiating the area of the triangle with respect to t and then solving it further for the maximum area we get the value of t and then we get the coordinate of F, then putting the point F in y = mx + 3 we get the value of m.

Complete step by step answer:
The equation of given parabola is ${{y}^{2}}=16x$.Here a = 4
Now let us assume that F $(4{{t}^{2}},8t)$ be a parametric point on the given parabola ${{y}^{2}}=16x$. Generally, equation of tangent to a parabola ${{y}^{2}}=4ax$ at $({{x}_{1}},{{y}_{1}})$ is given by $y{{y}_{1}}-2a(x+{{x}_{1}})=0$ , so here ${{x}_{1}}=4{{t}^{2}}\text{ and }{{y}_{1}}=8t$ and a = 4, so the equation of tangent to the parabola at point F is given by $y(8t)-2(4)(x+4{{t}^{2}})=0$ i.e. $x-yt+4{{t}^{2}}=0$. Now, since on y-axis x coordinate is 0, so putting x = 0, we have $-yt+4{{t}^{2}}=0\Rightarrow yt=4{{t}^{2}}\Rightarrow y=4t$ hence, this tangent will intersect y-axis at (0,4t). $\therefore G(0,4t)$

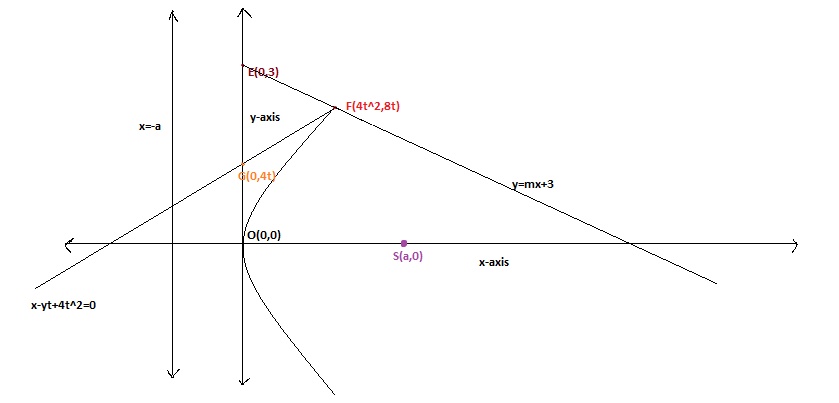
So, now we have E(0,3) , F $(4{{t}^{2}},8t)$ and G (0,4t).
Area of triangle $\Delta $ EFG (A) = \[\dfrac{1}{2}\left| \begin{matrix}
   0 & 3 & 1 \\
   0 & 4t & 1 \\
   4{{t}^{2}} & 8t & 1 \\
\end{matrix} \right|=\dfrac{1}{2}\left[ -3(-4{{t}^{2}})+1(-16{{t}^{3}}) \right]=\dfrac{1}{2}\left( 12{{t}^{2}}-16{{t}^{3}} \right)=6{{t}^{2}}-8{{t}^{3}}\]
$\therefore \text{A = }6{{t}^{2}}-\text{8}{{\text{t}}^{3}}$
Now, differentiating A with respect to t, we have
$\dfrac{dA}{dt}=12t-24{{t}^{2}}$ ………..(i)
For maximum or minimum A, $\dfrac{dA}{dt}=0\Rightarrow 12t-24{{t}^{2}}=0\Rightarrow 12t(1-2t)=0\Rightarrow t=0,\,1-2t=0\Rightarrow t=\dfrac{1}{2}$
$\therefore t=0,\dfrac{1}{2}$
Again, differentiating equation (i) with respect to t, we have
$\dfrac{{{d}^{2}}A}{d{{t}^{2}}}=12-48t$ ……(ii)
Putting t =0, in equation (ii) , we have, $\dfrac{{{d}^{2}}A}{d{{t}^{2}}}=12>0$
A is minimum at t = 0.
Now, putting $t=\dfrac{1}{2}$ in equation (ii), we have $\dfrac{{{d}^{2}}A}{d{{t}^{2}}}=12-48\left( \dfrac{1}{2} \right)=12-24=-12<0$
Therefore, A is maximum at $t=\dfrac{1}{2}$.
Hence , required value of t is $t=\dfrac{1}{2}$, now putting the value of $t=\dfrac{1}{2}$ in point F and G, we have, F (1,4) and G (0,2)
Now, since point F (4,1) passes through the line y = mx + 3, so it will satisfy this equation, so putting x = 1 and y = 4 in y = mx + 3, we have $4=m(1)+3\Rightarrow m=4-3=1$
$\therefore m=1$
Hence , the correct answer is option (4)

Note:
In order to solve any conic section problem, always try to draw a proper diagram, required as per the question and then proceed further, and must take care of the points to be drawn in the diagram. And always try to attack the question with the parametric form if the point at which tangent is to be drawn is not given.