Question

A line is drawn through the point (1, 2) to meet the coordinate axes at P and Q such that it forms a triangle OPQ where O is the origin. If the area of the triangle OPQ is least the slope of the line PQ is
       \[\begin{array}{l}
\left( {A.} \right)\,\,\, - 1\\
\left( B \right)\,\,\,\,\, - 2\\
\left( C \right)\,\,\,\,\, - \,\,\dfrac{1}{2}\\
\left( D \right)\,\,\,\,\, - \dfrac{1}{4}
\end{array}\]

Answer 1

Hint: Line is formed when two points are joined. It means a unique line can be drawn through 2 points. And there are infinites lines passing through a given point. Hence in this question it is given that the line is passing through a given point (1, 2). So firstly we can assume the most suitable form for line among 7 forms or line. Here we are using an intercept form \[\dfrac{x}{{OQ}} + \dfrac{y}{{OP}} = 1\]. Here OQ is the x –intercept and OP is the y intercept. PQ is the required line which makes the intercept with x and y axis. Since x-axis and y-axis are mutually perpendicular axis hence we have a right angle triangle.

Complete step by step solution:

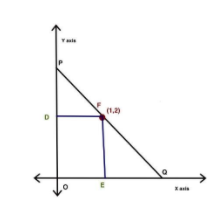
Step 1 From the above figure we can find segment AD by just applying the basic definition of .
\[\tan \theta = \dfrac{{perpendicular}}{{base}}\]
\[\tan \theta = \left( {\dfrac{{PD}}{{DF}}} \right) = \dfrac{{PD}}{1}\]
Step 2 from the figure
\[\tan \theta = \left( {\dfrac{{EF}}{{EC}}} \right) = \dfrac{2}{{EC}}\]
\[\begin{array}{l}
perpendicular = PD + OD\, = \tan \theta + 2\\
Base\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = OE + EQ\, = 1 + 2\cot \theta
\end{array}\]
Step 3 Area of the triangle OPQ is \[\dfrac{1}{2}\left( {2 + \tan \theta } \right)\left( {1 + 2\cot \theta } \right)\]
\[\begin{array}{l}
 = \dfrac{1}{2}\left( {2 + \tan \theta + 4\cot \theta + 2} \right)\\
 = \dfrac{1}{2}\left( {4 + \tan \theta + 4\cot \theta } \right)\\
 = \dfrac{1}{2}(4 + \ge 4)\\
 = \,\,4
\end{array}\]
Using inequality
 = In A.M –G.M inequality, equality holds when both numbers in A.P are equal. Here are equal
By equating \[\tan \theta \,and\,\cot \theta \,\]we get
\[\begin{array}{l}
\tan \theta \, = 4\cot \theta \\
{\tan ^2}\theta = 4\\
\therefore \,\,\tan \theta = \pm 2
\end{array}\]
\[\begin{array}{l}
hence\,slope\,of\,line\,is\,given\,by\,m\,which\,is\,equal\,to\,\tan \theta \\
and\,\,slope\,of\,line\,is\, \pm 2\\
but\,only\,\, - 2\,is\,given\,in\,the\,option
\end{array}\]
Hence the minimum area of the triangle OPQ is 4
Hence the slope of line is -2

Note: In case of triangle related questions and their area. Try to use different trigonometric angles relations like\[\tan \theta ,\cot \theta ,\cos \theta \,etc\]. A.M-G.M tools are often used to calculate the minimum value of the given numbers provided that number should be positive.