Question

A line intersecting a circle in two points is called a ____.
(a) Secant
(b) Chord
(c) Tangent
(d) None of these

Answer 1

Hint: Use the definition of each of the terms given in the options to find the line which intersects a circle in two points. Also, use the difference between a line and a line segment to find the correct answer.

Complete step by step answer:
We have to find the line which intersects a circle in two points.
We will use the definition of each of the terms given in the options.
Firstly, we will find the difference between a line and a line segment.
We know that a line is a straight set of points that extends in both directions without ending, as shown in the figure. It is of infinite length. Here, l is a line.

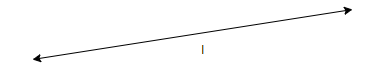
We know that a line segment is a part of a line between two endpoints. It is of finite length. Here, AB is a line segment.

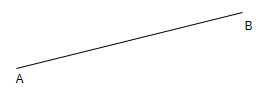
We will now consider each of the options.
We know that secant is any line that intersects the circle at two points, as shown in the figure. Here, line l intersects the circle at points A and B. Thus, it’s a secant.

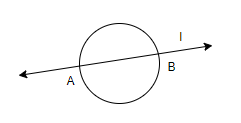
We know that chord is a line segment joining any two points on the circle, as shown in the figure. Here, AB is a chord of the circle.

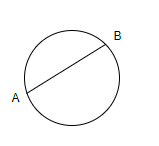
We know that tangent is a line that intersects the circle at one point and is perpendicular to the radius of the circle.
 

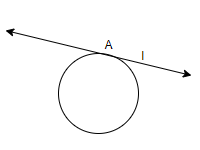
Thus, the line that intersects the circle at two points is secant.
Hence, the line intersecting the circle at two points is secant, which is option (a).

Note: One must keep in mind that we have to find the line intersecting a circle at two points. We have rejected the chord of the circle as the chord is a line segment, while secant is a line. If we consider the line and line segment as the same, we will get an incorrect answer.