Question

A light rod of length $ 200cm $ is suspended from the ceiling horizontally by means of two vertical wires of equal length tied to its ends. One of the wires is made of steel and is of cross-sectional area $ 0.1c{{m}^{2}} $ and the other is of brass of cross-sectional area $ 0.2c{{m}^{2}} $ . Find out the position along the rod at which weights may be hung to produce:
(a) equal stress in both wires
(b) equal strains in both wires.
 $ {{Y}_{steel}} $ = $ 20\times {{10}^{11}} $ dynes/ $ c{{m}^{2}} $ and $ {{Y}_{Brass}}=10\times {{10}^{11}} $ dynes.

Answer 1

Hint: In this problem we are having two wires one is made of steel and the other is made of copper. We know when load is attached to the wire then it may get stretched and the amount of extension depends upon the nature of the material used and can be quantified by Young’s Modulus. Both are having different cross-sectional areas.

Formula used
 $ Stress=\dfrac{F}{A} $ , where F is the force applied and A is the area
Young’s modulus, $ Y=\dfrac{Fl}{A\Delta l} $ , where L is the original length and $ \Delta l $ is the change in length.

Complete Step By Step Solution
We had depicted the situation in the figure below.

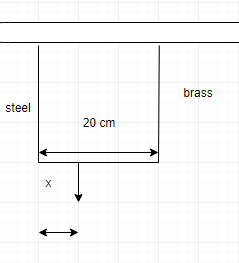
(a)
Let the load be hung at a distance of x cm from the steel wire end. Let the forces in steel and brass wires be $ {{F}_{1}} $ and $ {{F}_{2}} $ .
 $ \Rightarrow {{F}_{1}}x={{F}_{2}}(200-x) $
 $ \Rightarrow \dfrac{{{F}_{1}}}{{{F}_{2}}}=\dfrac{200-x}{x} $ --(1)
Also, $ Stress=\dfrac{F}{A} $
So, stress in steel wire $ =\dfrac{{{F}_{1}}}{0.1} $ $ =10{{F}_{1}} $ dynes/ $ c{{m}^{2}} $
So, stress in copper wire $ =\dfrac{{{F}_{2}}}{0.2} $ $ =5{{F}_{2}} $ dynes/ $ c{{m}^{2}} $
If the stress is equal, then,
 $ 5{{F}_{2}}=10{{F}_{1}} $
 $ \Rightarrow \dfrac{{{F}_{1}}}{{{F}_{2}}}=\dfrac{1}{2} $ --(2)
From equations (1) and (2) we get,
 $ \dfrac{1}{2}=\dfrac{200-x}{x} $
 $ \Rightarrow 400-2x=x \\
\Rightarrow 3x=400 \\
\Rightarrow x=\dfrac{400}{3} \\
\therefore x=133.33cm \\ $
(b) Let the weight w be hung at a point y cm away from the steel wire and forces developed in the steel brass wires be $ {{F}_{3}} $ and $ {{F}_{4}} $ respectively.
Therefore,
 $ {{F}_{3}}y={{F}_{4}}(200-y) \\
\Rightarrow \dfrac{{{F}_{3}}}{{{F}_{4}}}=\dfrac{(200-y)}{y} $ --(3)
Also, we know $ Y=\dfrac{Fl}{A\Delta l} $ and strain is $ \dfrac{\Delta l}{l} $ , so from these two we can write the strain as
  $ \Rightarrow \dfrac{\Delta l}{l}=\dfrac{F}{AY} $
Now, strain in steel wire must be equal to strain in brass wire, thus
 $ \Rightarrow \dfrac{{{F}_{3}}}{0.1{{Y}_{steel}}}=\dfrac{{{F}_{4}}}{0.2{{Y}_{brass}}} \\
\Rightarrow \dfrac{{{F}_{3}}}{0.1\times 20\times {{10}^{11}}}=\dfrac{{{F}_{4}}}{0.2\times 10\times {{10}^{11}}} \\ $
 $ \therefore \dfrac{{{F}_{3}}}{{{F}_{4}}}=1 $ ---(4)
From equations (3) and (4) we get,
 $ Y=100cm $ .

Note:
For the wires of the same material young’s modulus is the same as young’s modulus of elasticity depending upon the nature of material of the substance. If the material of the wires is different than their values of young’s modulus will also be different. Young’s modulus is the property of the material which measures the elasticity of the material. Strain is a unitless quantity.