Question

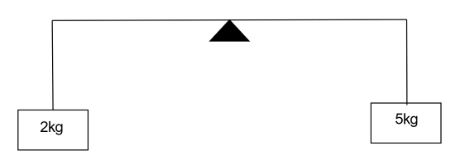
A light rod of length \[1m\] is pivoted at its center and two masses of \[5\,kg\] and \[2\,kg\] are hung from the ends as shown in the figure. Find the initial angular acceleration of the rod assuming that it was horizontal in the beginning.
A. \[8.4\,rad/{s^2}\]
B. \[2\,rad/{s^2}\]
C. \[1\,rad/{s^2}\]
D. \[5\,rad/{s^2}\]

Answer 1

Hint: We are asked to find the initial angular acceleration of the rod. We can start by noting down the data given in the question. We can then find the total torque of the motion by subtracting the initial torque from the final torque. We can then equate this to another formula of torque involving the net moment of inertia and angular acceleration, thus solving the question and giving us the required solution.

Formulas used:
Torque is given by two formulas,
One of the formulas to find the torque is given as,
\[\tau = r \times F\]
The second formula is given as,
\[\tau = I\alpha \]
Where \[I\] is the moment of inertia of the motion, \[\alpha \] is the angular acceleration of the motion, \[r\] is the length and \[F\] is the force.

Complete step by step answer:
The following data is given in the question,
One of the masses hung from the rod are \[{m_1} = 2\,kg\]
The second mass hanging from the rod is given as, \[{m_2} = 5\,kg\]
The rod is let to pivot on the centre hence giving the length to be \[{r_1} = {r_2} = \dfrac{1}{2}\].
Now that we have written down the data in the question, we can move onto finding the value of torque using the formula, \[\tau = r \times F\]. That is
\[\tau = {r_2} \times {F_2} - {r_1} \times {F_1} \\
\Rightarrow \tau = \dfrac{1}{2} \times 5g - \dfrac{1}{2} \times 2g \\
\Rightarrow \tau = \dfrac{3}{2}g\]

This value can be equated with,
\[\tau = I\alpha \]
\[\Rightarrow \dfrac{3}{2}g = I\alpha \]
The value of angular acceleration can be found out as,
\[\alpha = \dfrac{{3 \times g}}{{2 \times I}} \\
\Rightarrow \alpha= \dfrac{{3 \times 9.8}}{{2 \times I}}\]
The value of moment of inertia is,
\[I = m{r^2} \\
\Rightarrow I = 5kg{\left( {\dfrac{1}{2}} \right)^2} + 2kg{\left( {\dfrac{1}{2}} \right)^2} \\
\Rightarrow I = \dfrac{7}{4}\]

The angular momentum can be found out as,
\[\alpha = \dfrac{{3 \times g}}{{2 \times I}} \\
\Rightarrow \alpha = \dfrac{{3 \times 9.8}}{{2 \times I}} \\
\Rightarrow \alpha = \dfrac{{3 \times 9.8 \times 4}}{{2 \times 7}} \\
\therefore \alpha = 8.4\,rad/{s^2}\]

Therefore, the right answer is option (A).

Note: The force is found as the product of mass and acceleration. The acceleration of the masses is taken as the acceleration due to gravity because the masses are suspended from the rod and the acceleration is downwards. A quantity expressing a body's tendency to resist angular acceleration is the sum of the products of the mass of each particle in the body with the square of its distance from the axis of rotation.