Question

A light beam, emanating from the point (3, 10) reflects from the straight line $2x+y-6=0$ and then passes through the point (7, 2). Find the equation of the incident and reflected ray.

Answer 1

Hint: First we will draw the figure. Now we know that angle of incidence = angle of reflection hence the normal to the line 2x + y – 6 = 0 at intersection point of incident ray and reflected ray will be the angle bisector of angles made by incident ray and reflected ray. Now we will consider the two triangles formed and prove them to be congruent by the SAS test. Hence we will get the normal intersects line joining (3, 10) and (7, 2) at midpoint. Now we can easily find the coordinate of midpoint by midpoint formula which is $\left(\dfrac{{{x}_{1}}+{{y}_{1}}}{2},\dfrac{{{x}_{2}}+{{y}_{2}}}{2} \right)$ . Now we can also find the foot of perpendicular from this midpoint to the line 2x + y – 6 = 0. Hence we will get the coordinates of the point of intersection of incident ray and reflected ray. Now using the equation of line in two point form we can find the equation of incident line and reflected line.

Complete step by step answer:

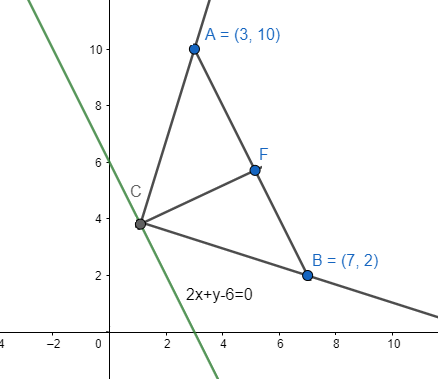
Now we know that the light beam starts at point (3, 10) let us call this point as A. Now let us say, it reflects at point C on line $2x+y-6=0$ and then the reflected ray passes through point
(7, 2) let us call this point B. Now let CF perpendicular to the line $2x+y-6=0$ at point C.
Now CF is the angle bisector to $\angle ACB$ .
Hence we get $\angle ACF=\angle BCF$ .
Now let this angle be $\theta $ .
Now we have $AC=CF\cos \theta $ and $CB=CF\cos \theta $ hence we have $CB=AC$
Now in triangle ACF and triangle BCF we have
CF = CF, $\angle ACF=\angle BCF$ and CB = AC.
Hence from SAS test we get the triangles are congruent.
Hence we get AF = BF.
Now hence we get that F is mid-point of AB.
Now we know that midpoint of $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ is given by $\left( \dfrac{{{x}_{1}}+{{y}_{1}}}{2},\dfrac{{{x}_{2}}+{{y}_{2}}}{2} \right)$
Hence mid-point of A = (3, 10) and B = (7, 2) is
$\left( \dfrac{7+3}{2},\dfrac{10+2}{2} \right)=\left( 5,6 \right)$
Hence we get the coordinate of F is (5, 6).
Now we consider the line $2x+y-6=0..................\left( 1 \right)$
Rearranging the terms we get $y=-2x+6$
Now if we compare the equation with slope intercept form which is y = mx + c we get the slope of line is – 2.
Now we know that product of slopes of perpendicular lines is – 1.
Let us say the slope of CF be m.
Hence we get
$\begin{align}
  & \left( -2 \right)m=-1 \\
 & \therefore m=\dfrac{1}{2} \\
\end{align}$
Now equation of line in CF in slope point form is
$\begin{align}
  & y=\dfrac{1}{2}x+c \\
 & \Rightarrow 2y=x+2c \\
\end{align}$
Now we know that this line passes through F.
Hence substituting the coordinates of F we get
$\begin{align}
  & 2\left( 6 \right)=5+2c \\
 & \Rightarrow 12=5+2c \\
 & \therefore c=\dfrac{7}{2} \\
\end{align}$
Hence we get equation of CF is
$\begin{align}
  & y=\dfrac{1}{2}x+\dfrac{7}{2} \\
 & \Rightarrow 2y=x+7 \\
\end{align}$
Hence Now we have equation of line CF is 2y = x + 7.
Now multiplying the equation by 2 and rearranging we get 2x - 4y + 14 = 0. ………………… (2)
Now point C is nothing but intersection of CF and the line $2x+y-6=0$
Now we will solve the equation simultaneously to find point C. hence subtracting equation (2) from equation (1) we get
Hence we get 2x + y – 6 – 2x + 4y – 14 =0
Hence 5y – 20 = 0
Hence we get y = 4.
Now substituting y = 4 in equation (1) we get
2x+ 4 – 6 = 0 Hence solving this we get x = 1.
Hence the coordinate of point C is (1, 4).
Now let us find the equation of AC
We have A = (3, 10) and C = (1, 4)
Now we know that equation of line passing through $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ is given by $\dfrac{y-{{y}_{1}}}{{{y}_{1}}-{{y}_{2}}}=\dfrac{x-{{x}_{1}}}{{{x}_{1}}-{{x}_{2}}}$
Hence the equation of line passing through (3, 10) and (1, 4) is
$\begin{align}
  & \dfrac{x-3}{3-1}=\dfrac{y-10}{10-4} \\
 & \Rightarrow x-3=2 \times \dfrac{y-10}{6} \\
 & \Rightarrow 3x-9=y-10 \\
 & \Rightarrow 3x-y+1=0 \\
\end{align}$
Hence the equation of incident ray is 3x – y + 1 = 0.
Now similarly consider the equation of line passing through (7, 2) and (1, 4) is given by
$\begin{align}
  & \dfrac{x-7}{7-1}=\dfrac{y-2}{2-4} \\
 & \Rightarrow \dfrac{x-7}{6}=\dfrac{y-2}{-2} \\
 & \Rightarrow -2x+14=6y-12 \\
 & \Rightarrow 2x+6y-26=0 \\
\end{align}$

Hence the equation of refracted ray is 2x + 6y – 26 = 0.

Note: Now we can also solve this question by using formula for point of reflection about the line let A’ and B’ be the reflections of point A and B. Now the reflection of point $({{x}_{1}},{{y}_{1}})$ with respect to line ${{a}_{1}}x+{{b}_{1}}y+c=0$ is (x, y) then (x, y) is given by, $\dfrac{x-{{x}_{1}}}{a}=\dfrac{y-{{y}_{1}}}{b}=\dfrac{2\left( {{a}_{1}}{{x}_{1}}+{{b}_{1}}{{y}_{1}}+c \right)}{{{a}_{1}}^{2}+{{b}_{1}}^{2}}$ . Now the line of incident is the line passing through AB’ and the reflected line is the line passing through A’B. We can easily find the equation of lines with the help of two point form.