Question

A lift is moving with a uniform downward acceleration of $2m/{{s}^{2}}$. A ball is dropped from a height 2 m from the floor of lift. Find the time taken after which ball will strike the floor?( $g=10m/{{s}^{2}}$).

$\begin{align}
  & \text{A}\text{. }\sqrt{2}\sec \\
 & \text{B}\text{. 2 sec} \\
 & \text{C}\text{. }\dfrac{1}{2}\sec \\
 & \text{D}\text{. }\dfrac{1}{\sqrt{2}}\sec \\
\end{align}$

Answer 1

Hint: At first we need to draw the diagram according to the question, now we will have to find the acceleration of the ball if the lift is stationary. We can take it from the perspective of a man standing inside the lift. Now with this acceleration apply the equation of motion to find the required result.

Formula used:
${{a}_{bf}}={{\vec{a}}_{b}}-{{\vec{a}}_{f}}$
$y=ut+\dfrac{1}{2}a{{t}^{2}}$

Complete step by step answer:
In the above diagram drawn we see a, lift which is going down with a downward acceleration of $2m/{{s}^{2}}$, Now a ball is dropped o released from a height of 2cm, as the ball is released so the ball will move with an acceleration of $g\text{ }m/{{s}^{2}}$ that is the acceleration due to the gravity of the earth.
Therefore the motion of the ball can be called a motion under gravity.
Now the acceleration of the floor and the ball is , ${{a}_{f}}=-2\hat{j}$ and ${{a}_{b}}=-g\text{ }\hat{j}$ respectively.
In this question it is given that $g=10m/{{s}^{2}}$.
Now, if we consider a man standing in the lift and we are considering that the ball is falling from the perspective on the man, so

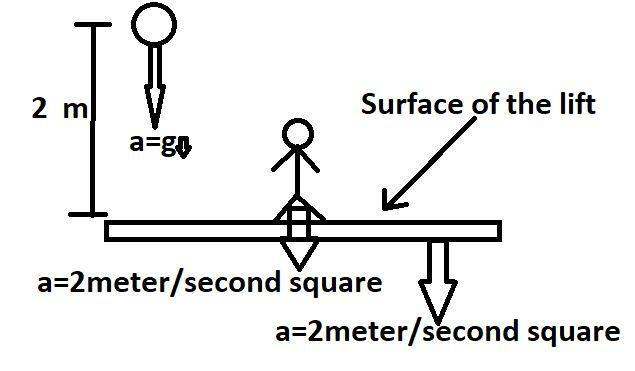
In the above diagram, the man is also moving downwards with an acceleration of $2m/{{s}^{2}}$.
Now, if we find the acceleration of the ball with respect to floor,
${{a}_{bf}}={{\vec{a}}_{b}}-{{\vec{a}}_{f}}$
${{a}_{bf}}=-g\text{ }\hat{j}-\left( -2\hat{j} \right)$,
${{a}_{bf}}=-10\hat{j}-\left( -2\hat{j} \right)$,
Now, we get the acceleration of ball with respect to floor as ,
${{a}_{bf}}=-8\hat{j}$.

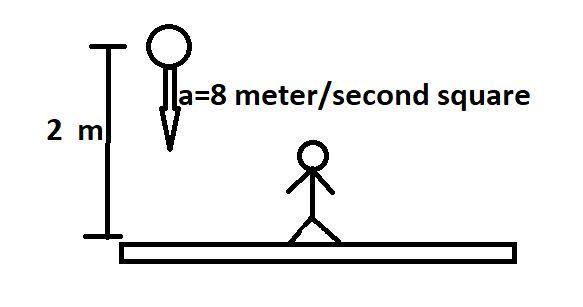
In the above diagram, we see that the lift has become stationary and the ball is falling with an acceleration of $8m/{{s}^{2}}$.
Now, using equation of motion,
$y=ut+\dfrac{1}{2}a{{t}^{2}}$,
Considering downward direction as positive and upward direction as negative.
$2=0+\dfrac{1}{2}\times 8\times {{t}^{2}}$,
$t=\dfrac{1}{\sqrt{2}}$ seconds, therefore option D is the correct option.

Note:
When we are finding the acceleration of the ball with respect to the floor of the lift we actually find the acceleration from the perspective of the observer. In this value of acceleration according to the observer, he is in a stationary position and only the ball is moving.