Question

What is a lens formula? Derive the formula $\dfrac{1}{v}-\dfrac{1}{u}=\dfrac{1}{f}$ for spherical lenses.

Answer 1

Hint: Lens formula is the relationship between the distance of an object $u$, distance of image $v$ and the focal length of the lens $f$. This law can be used for both concave and convex lenses with appropriate sign conventions. Using similarity of triangles we can prove the following.

Formula used: $\dfrac{1}{v}-\dfrac{1}{u}=\dfrac{1}{f}$

Complete step-by-step answer:
Lens formula is the relationship between the distance of an object $u$, distance of image $v$ and the focal length of the lens $f$. This law can be used for both concave and convex lenses with appropriate sign conventions. The thickness of the lens is neglected.

Lens formula: $\dfrac{1}{v}-\dfrac{1}{u}=\dfrac{1}{f}$

The diagram below shows the formation of a real, inverted and diminished image of \[\text{AB}\]. Where \[\text{AB}\] is placed beyond the center of curvature.

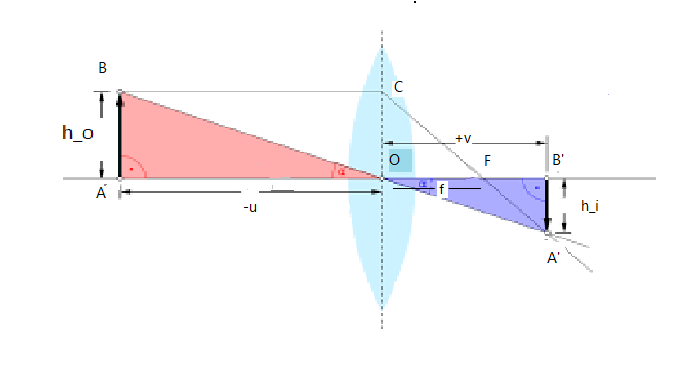
Here object distance $OB =-u$, image distance $OB\prime=+v$ and focal length $OF=f$

Clearly $\Delta ABO \cong \Delta A\prime B\prime$
Therefore $\dfrac{A\prime B\prime}{AB}=\dfrac{OB\prime}{OB}$
Also $\Delta ABF \cong \Delta OCf$
Therefore $\dfrac{A\prime B\prime}{OC}=\dfrac{FB\prime}{OF}$, but $OC=AB$

Then, $\dfrac{A\prime B\prime}{AB}=\dfrac{FB\prime}{OF}$
Therefore $\dfrac{A\prime B\prime}{AB}=\dfrac{OB\prime}{OB}=\dfrac{FB\prime}{OF}$
$\dfrac{OB\prime}{OB}=\dfrac{FB\prime}{OF}= \dfrac{OB\prime-OF}{OF}$

Substituting using sign conventions

$\dfrac{v}{-u}=\dfrac{v-f}{f}$
$vf=-uv+uf $ or $uv=f(u-v)$

Dividing both sides by $uvf$

$\dfrac{uv}{uvf}=\dfrac{fu}{uvf}-\dfrac{fv}{uvf}$
$\dfrac{1}{f}=\dfrac{1}{v}-\dfrac{1}{u}$

Additional Information:
The formula is called the thin lens formula or Lensmaker’s equation. This is used to make commercial lenses such as magnifying glasses and spectacles.

To identify the nature of the object, like magnification, magnification equation is used which states $M=\dfrac{Height\; of \;image}{Height\; of \;object}=-\dfrac{distance\; of\; image}{distance\; of\; object}$ if $M=+$ then the image is magnified and if $M=-$ then image is diminished.

Note:
The thickness of the lens is neglected. Be aware of the sign conventions and the triangles selected. Remember how is lens law defined and its formula $\dfrac{1}{f}=\dfrac{1}{v}-\dfrac{1}{u}$. The formula can be used for any lens and when the object is placed is anywhere on the principal axis.