Question

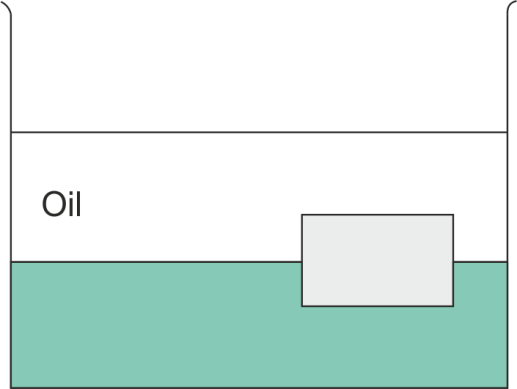
A layer of oil with density $724\text{ kg/}{{\text{m}}^{3}}$ floats on water of density $1000\text{ kg/}{{\text{m}}^{3}}$. A block floats at the oil water interface with $\dfrac{1}{6}$ of its volume in oil and $\dfrac{5}{6}$ of its volume in water as shown in the figure. What is the density of the block?

(A) $1024\text{ kg/}{{\text{m}}^{3}}$
(B) $1276\text{ kg/}{{\text{m}}^{3}}$
(C) $776\text{ kg/}{{\text{m}}^{3}}$
(D) $951\text{ kg/}{{\text{m}}^{3}}$

Answer 1

Hint: Oil molecules are only attracted to other oil molecules. Water is more dense than oil; they can’t mix oil floats above the water. Density is the weight of a substance for a specific volume.
Density$=\dfrac{mass}{volume}$, $volume\times density=mass$
Formula used:
By using Archimedes Principle
Upthrust $=$ Weight of the liquid displaced.
$\left( {{V}_{Pb}} \right)g=\left( {{V}_{o{{\rho }_{1}}}} \right)g+\left( {{V}_{W{{\rho }_{2}}}} \right)g$
$\left( {{V}_{Pb}} \right)g\to $Volume of block $\times $density of block $\times $ specific gravity.
$g\to $specific gravity
${{V}_{0}}\to $ Volume of oil.
${{\rho }_{1}}\to $ Density of oil
${{V}_{w}}\to $ Volume of water
${{\rho }_{2}}\to $ Density of water
Complete solution:
Given data:
Density of oil ${{\rho }_{1}}=724\text{ kg/}{{\text{m}}^{3}}$
Density of water ${{\rho }_{2}}=1000\text{ kg/}{{\text{m}}^{3}}$
According to Archimedes principle
Upthrust $=$ Weight of liquid displaced
${{\left( {{V}_{\rho }} \right)}_{b}}g={{V}_{0}}{{\rho }_{1}}g+{{V}_{w}}{{\rho }_{2}}g$
$\Rightarrow {{\left( {{V}_{\rho }} \right)}_{b}}g=\dfrac{V}{6}\left( 724 \right)g+\dfrac{5V}{6}\left( 1000 \right)g$
Where, ${{V}_{b}}\to $ block volume, ${{\rho }_{b}}\to $ density of block
${{V}_{0}}=\dfrac{V}{6},{{V}_{\infty }}=\dfrac{5V}{6}$
$\Rightarrow {{\left( {{V}_{\rho }} \right)}_{b}}g=\left( \dfrac{724V}{6}+\dfrac{5000V}{6} \right)g$
${{\left( V\rho \right)}_{b}}=\dfrac{724V}{6}+\dfrac{5000V}{6}$
$V{{\rho }_{b}}=\dfrac{5724}{6}V$
${{\rho }_{b}}=\dfrac{5724}{6}$
${{\rho }_{b}}=954\text{ kg/}{{\text{m}}^{3}}$

Therefore the density of the block is $954\text{ kg/}{{\text{m}}^{3}}$ i.e. option (d) is correct.

Additional information:
Density of liquid water is $1\text{ g/c}{{\text{m}}^{3}}$ and vegetable oil is $0.93\text{ g/c}{{\text{m}}^{3}}$. Ice has a density of $0.92\text{ g/c}{{\text{m}}^{3}}$ Which is why it floats on water and oil.

Note:
Oil is less dense than water. The molecules that make the oil are larger than those that make up water, so they cannot pick as tightly together as the water molecules.