Question

A lawn roller in the form of a thin-walled hollow cylinder of mass M is pulled with a constant horizontal force F applied by a handle attached to the axle.
It rolls without shipping.
(A) The frictional force $F/2$
(B) Acceleration is $F/2M$
(C) Acceleration is $F/M$
(D) The frictional force is $3F/4$

Answer 1

Hint:To solve this type of problem we have to show the picture of the information. Then by applying proper formulas we can solve the problem. Here use a lavish holler so inertia is applied.

Complete step by step answer:
Definition:
Torque is the tendency of a force to rotate the body to which it is applied.
\[\tau = I\alpha \]
There are two types of acceleration, linear acceleration and angular acceleration. For a pure rolling system the linear acceleration is zero and for a pure horizontal motion the angular acceleration will be zero.
Given, mass of cylinder\[ = {\text{ }}M\]
Horizontal force or applied force \[ = F.\]
So the free body diagram is,

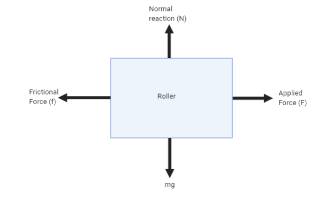
Let, be the angular acceleration, Risa constant of them, we can write
Angular acceleration,\[\alpha \]is,
\[\alpha = \dfrac{{d\omega }}{{dt}}\]
And
Velocity,v is
\[v = r\omega \]
From this we need to find relation between linear and angular acceleration,
\[
\dfrac{{dv}}{{dt}} = r\dfrac{{d\omega }}{{dt}}.\omega \dfrac{{dr}}{{dt}} \\
\\
 \]
Since r is constant,
\[\dfrac{{dr}}{{dt}} = 0\]
So ,
\[\dfrac{{dv}}{{dt}} = r\dfrac{{d\omega }}{{dt}}\]
Here \[\dfrac{{dv}}{{dt}}\]= linear acceleration, \[\dfrac{{d\omega }}{{dt}}\] = angular acceleration
So,
\[a = r\alpha \]
\[a = R\alpha {\text{ }}\left( {for{\text{ }}no{\text{ }}slipping} \right)\]
where a is linear acceleration.
Again, we know, \[\tau = fR = I\alpha \]
Where f is frictional force, \[I\]is Inertia, and \[\tau \] is the torque.
The moment of inertia of this system is,
\[I = M{R^2}\]
Then we can write.
\[fR = M{R^2}\alpha \]

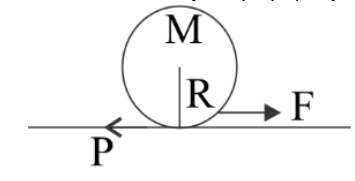
\[\therefore I = M{R^2}\] for a cylinder having mass \[M\] and radius \[R.\]
\[F = MR\alpha \]
Again, we know, \[{f_{total}} = Ma\] by the Newton law of motion.
\[\therefore Ma = F - f\]
\[\therefore Ma = F - ma\]
\[2Ma = F\]
\[a = \dfrac{F}{{2M}}\]
\[\therefore practical\;{\text{force f = M}}{\text{.a}}{\text{.}}\]
\[{\text{ = M}}{\text{.}}\dfrac{F}{
2M \\
  \\
 }\]
\[ = \;F/2\]
\[\therefore \] option \[A\] and \[B\] both are true.

Note:To know about this solution. We have to know about the relation between angular and linear acceleration, force, inertia, etc. If we got to know about their relationship then we can find out the problem. Also we have to drain the relation picture of the current then we get to know which force applied in which direction.