Question

A large weather balloon whose mass is $226{\text{kg}}$ filled with helium gas until its volume is $325{{\text{m}}^3}$. Assume the density of air is $1.2{\text{kg}}{{\text{m}}^{ - 3}}$ and the density of helium is $0.179{\text{kg}}{{\text{m}}^{ - 3}}$. What additional mass can the balloon support in equilibrium?

Answer 1

Hint:To solve such problems we need to draw a free body diagram to know all the components of force acting on the body so that we do not miss out any and as we have to find the additional mass in equilibrium, therefore, we need to balance all the force acting on it.

 Complete step by step solution:
The given values in the question are
Mass $ = 226{\text{kg}}$, let this be ${M_b}$
Volume $ = 325{{\text{m}}^3}$, let this be $V$
The density of air $ = 1.2{\text{kg}}{{\text{m}}^{ - 3}}$ , let this be ${\rho _{air}}$
The density of helium $ = 0.179{\text{kg}}{{\text{m}}^{ - 3}}$ , let this be ${\rho _h}$
And $g$ be the acceleration due to gravity
Now let us draw the free body diagram of the balloon and denote the force acting on it

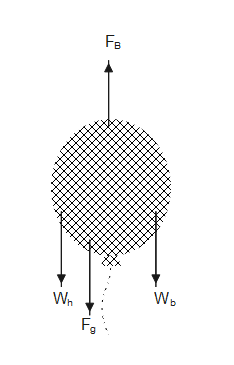
Where, ${F_B}$ is Buoyant force, ${W_h}$ is the weight of helium, ${W_b}$ is the weight of the balloon and ${F_g}$ is the gravitational force.
So the total force along the Y-axis $(\Sigma {F_y})$ will be zero as the system is in equilibrium.
$ \Rightarrow \Sigma {F_y} = {F_B} - {W_h} - {W_b} - {F_g} = 0$
$ \Rightarrow \Sigma {F_y} = \Sigma {F_N} - {F_g} = 0$
Where, $\Sigma {F_N}$ is the net force which will be,
$ \Rightarrow \Sigma {F_N} = {F_B} - {W_h} - {W_b} - - - - (1)$
Now we know, ${F_B} = {\rho _a} \times V \times g$
Substituting the values we get,
$ \Rightarrow {F_B} = 1.2 \times 325 \times 9.8$
$ \Rightarrow {F_B} = 3822{\text{N}} - - - (2)$
And ${W_h} = {\rho _h} \times V \times g$
Substituting the values we get,
$ \Rightarrow {W_h} = 0.179 \times 325 \times 9.8$
$ \Rightarrow {W_h} = 570{\text{N}} - - - (3)$
And ${W_b} = {M_b} \times g$
Substituting the values we get,
$ \Rightarrow {W_b} = 226 \times 9.8$
$ \Rightarrow {W_b} = 2214.8{\text{N}} - - - (4)$
Now putting the values from equations (2),(3) and (4) in (1), we get
 $ \Rightarrow \Sigma {F_N} = 3822 - 570 - 2214.8$
$ \Rightarrow \Sigma {F_N} = 1.037 \times {10^3}{\text{N}}$
Therefore using the above value in the total force along with the Y-axis equation, we get
$ \Rightarrow \Sigma {F_y} = 1037 - {F_g} = 0$
$ \Rightarrow {F_g} = 1037$
Now we know ${F_g} = M \times g$
Where $M$ is the additional mass in equilibrium that we need to find out
$ \Rightarrow M = \dfrac{{1037}}{g}$
Substituting the value of acceleration due to gravity $g = 9.8 m/s^2 $ we get,
$ \therefore M = 105{\text{kg}}$
Therefore the mass $105.8{\text{kg}}$ can be supported by the balloon in equilibrium.

Note: Buoyant force accounts for the air buoyancy created by the displaced air similar to the displacement of liquid in case of submerged body underwater and it acts downwards. Note the calculation of the weight of helium and the balloon which is equal to the mass multiplied by the acceleration due to gravity.