Question

A large flat metal surface has a uniform charge density $\left( { + \sigma } \right)$. An electron of mass m and charge $\rho $leaves the surface at point A with speed u and returns to it at point B. Disregarding gravity, the maximum value of AB is:

A) $\dfrac{{2{\mu ^2}m{\varepsilon _0}}}{{\sigma \rho }}$
B) \[\dfrac{{{\mu ^2}.\rho {\varepsilon _0}}}{{\mu \rho }}\]
C) \[\dfrac{{{\mu ^2}\rho }}{{{\varepsilon _0}m\sigma }}\]
D) $\dfrac{{{\mu ^2}\sigma \rho }}{{\varepsilon .m}}$

Answer 1

Hint: The electron releasing is a projectile and its trajectory (path) is parabolic due to the electric force acting downward on the electron because of the positively charged plate. The maximum value of AB can be decided by how far the electron can go when released from the surface which is given by its range.
$R = \dfrac{{{u^2}\sin 2\theta }}{g}$
Electric field (E) for uniform surface is $\dfrac{\sigma }{{2{\varepsilon _0}}}$
Other relationships that can be used are:
F = ma
F = qE

Complete step by step answer:
When the electron is released from point A, it will move in a parabolic path as the force on the electron will be downwards at all the points since the electron is negatively charged and the surface is positively charged. Diagrammatically:

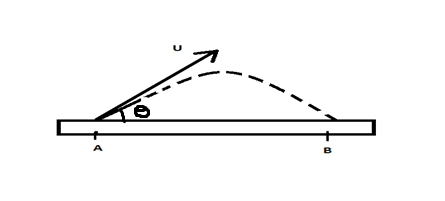
The maximum value of AB is given by the maximum range of this projectile
 Range (R) of a projectile is given as:
$R = \dfrac{{{u^2}\sin 2\theta }}{g}$
Maximum value of $\sin \theta $ = 1 at $\theta = {90^ \circ }$
But here we have $\sin 2\theta $, the angle will become:
$2\theta = {90^ \circ }$
$\theta = {45^ \circ }$
Now, $\sin 2\theta $ = 1
Maximum range is given as:
$R = \dfrac{{{u^2}}}{g}$
But we have to disregard gravity (given in the question), so instead of considering acceleration due to gravity ‘g’ we will consider the acceleration due to electric force ‘a’. So,
$R = \dfrac{{{u^2}}}{a}$ _______ (1)
From newton’s second law of motion:
F = ma
$a = \dfrac{F}{m}$ ____________ (2)
Force in terms of charge and electric field is:
F = qE ______________ (3)
Electric field for uniform surface is $\dfrac{\sigma }{{2{\varepsilon _0}}}$, charge of electron be e, equation (3) becomes:
F = $\dfrac{{e\sigma }}{{2{\varepsilon _0}}}$
Substituting this value in (2), we get:
$a = \dfrac{{e\sigma }}{{2{\varepsilon _0}m}}$
Therefore, the acceleration due to electric force is $\dfrac{{e\sigma }}{{2{\varepsilon _0}m}}$
Replacing this value of a in (1) to get maximum range:
$R = \dfrac{{{u^2}}}{{\left( {\dfrac{{e\sigma }}{{2{\varepsilon _0}m}}} \right)}}$
$R = \dfrac{{2{\mu ^2}m{\varepsilon _0}}}{{\sigma \rho }}$
Therefore, the maximum value of AB is \[\dfrac{{2{\mu ^2}m{\varepsilon _0}}}{{\sigma \rho }}\] and thus the correct option is A).

Note:When an object is projected in the air, it is called a projectile and the path it covers is called trajectory.
The parabolic path is covered by a projectile when a downward force is acting on the body at all its points during the motion.
The range can be defined as the distance that the projectile covers