Question

A landmark on the bank of the river is observed from two points A and B on the opposite bank of the river. The lines of sight make equal angles of with the bank of the river. If AB is 3 km, then the width of the river (in kilometer) is:
A) 2 km
B) \[\dfrac{1}{2}\]km
C) \[\dfrac{{\sqrt 3 }}{2}\] km
D) \[\dfrac{{\sqrt 2 }}{2}\] km

Answer 1

Hint: First find the distance BC or CA by congruency then use trigonometry ratio \[\tan \theta = \dfrac{{{\text{Perpendicular}}}}{{{\text{Base}}}}\] to find DC as perpendicular is DC, base is CA which is computed earlier and angle \[30^\circ \] is provided.

Complete step-by-step answer:
First, we will draw the figure to understand the question,

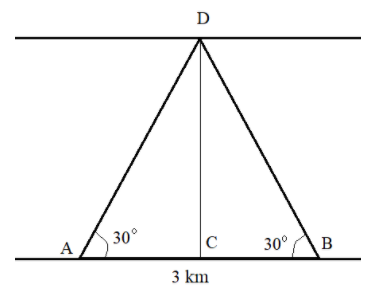
From the figure width of the river is DC means we have to find the distance DC.
We know the distance between A and B but first we have to find distance CB or AC to reach
our goal. For this we will prove triangle ACD and triangle DCB are congruent.
After analyzing the triangle ACD and triangle DCB we get the following results,
Angle A and angle B is same, \[\angle A = \angle B = 30^\circ \]
Angle C is right angle triangle in both the triangles, \[\angle ACD = \angle BCD\]
And DC is common, \[DC = CD\]
Thus, from these results we conclude that ACD and triangle DCB are congruent triangles by
AAS rule, so AC is equal to CB.
Now, we can divide distance AB by two to get the distance AC or CB.
\[AC = CB = \dfrac{3}{2}\]
Now we know a side and the angle so we can apply a trigonometric ratio to find the width of the river.
As we know that, \[\tan \theta = \dfrac{{{\text{Perpendicular}}}}{{{\text{Base}}}}\] and we have the value of and base and have to find perpendicular so, this trigonometry is best fit to find DC.
Now we are applying this trigonometric ratio into the triangle DCB and substituting the values into trigonometric ratio,
\[
  \tan 30^\circ = \dfrac{{{\text{DC}}}}{{{\text{CB}}}} \\
  \tan 30^\circ = \dfrac{{{\text{2DC}}}}{{\text{3}}} \\
\]
From this we can find DC as,
 \[DC = \dfrac{{3\tan 30^\circ }}{2}\]
We know that \[\tan 30^\circ = \dfrac{{\text{1}}}{{\sqrt 3 }}\], substituting this in the last result, we get
\[
  DC = \dfrac{3}{{2\sqrt 3 }} \\
   = \dfrac{{\sqrt 3 \cdot \sqrt 3 }}{{2\sqrt 3 }} \\
   = \dfrac{{\sqrt 3 }}{2} \\
\]
Thus, the width of the river is \[\dfrac{{\sqrt 3 }}{2}\] km.
Hence option C is correct.

Note: Any of the trigonometric functions can be used to find the answer but while solving these questions we have to first focus on “what we have to find” and then on “what data we have” so make our calculation shorter.