Question

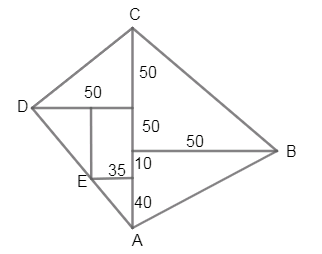
A land surveyor records the various treatments of a field in his measurement book as given below. The area of the field surveyed is (all readings are in meters):

(a) 6000 sq. m
(b) 7000 sq. m
(c) 7500 sq. m
(d) 8250 sq. m

Answer 1

Hint: In this question, we first need to name the various fields. Then find each of the areas of the field using the formula for the area of a right angled triangle given by \[\dfrac{1}{2}bh\]and the area of a rectangle is given by the formula \[lb\]. Now, add all the corresponding areas of each of the field to get the area of the complete field

Complete step by step answer:
As we already know that the area of a right angled triangle is given by the formula
\[\dfrac{1}{2}bh\]
Where, b is the base and h is the height
Now, the area of a rectangle of length l and breadth b is given by the formula
\[lb\]
Now, let us find the areas of each of the triangles and rectangle using the respective formulae

Now, on considering the right angled triangle (1) we have
\[b=50,h=50\]
Now, from the formula of area of a triangle we have
\[\Rightarrow \dfrac{1}{2}bh\]
Now, on substituting the respective values we get,
\[\Rightarrow \dfrac{50\times 50}{2}\]
Now, on further simplification we get,
\[\Rightarrow 1250\]sq. m
Now, on considering the right angled triangle (2) we have
\[b=50,h=100\]
Now, from the formula of area of a triangle we have
\[\Rightarrow \dfrac{1}{2}bh\]
Now, on substituting the respective values we get,
\[\Rightarrow \dfrac{50\times 100}{2}\]
Now, on further simplification we get,
\[\Rightarrow 2500\]sq. m
Let us now consider the right angled triangle (3) we have
\[b=50,h=50\]
Now, from the formula of area of a triangle we have
\[\Rightarrow \dfrac{1}{2}bh\]
Now, on substituting the respective values we get,
\[\Rightarrow \dfrac{50\times 50}{2}\]
Now, on further simplification we get,
\[\Rightarrow 1250\]sq. m
Let us now consider the rectangle (4) we have
\[l=60,b=35\]
Now, from the formula of area of a triangle we have
\[\Rightarrow lb\]
Now, on substituting the respective values we get,
\[\Rightarrow 60\times 35\]
Now, on further simplification we get,
\[\Rightarrow 2100\]sq. m
Now, on considering the right angled triangle (5) we have
\[b=40,h=35\]
Now, from the formula of area of a triangle we have
\[\Rightarrow \dfrac{1}{2}bh\]
Now, on substituting the respective values we get,
\[\Rightarrow \dfrac{40\times 35}{2}\]
Now, on further simplification we get,
\[\Rightarrow 700\]sq. m
Now, on considering the right angled triangle (6) we have
\[b=60,h=15\]
Now, from the formula of area of a triangle we have
\[\Rightarrow \dfrac{1}{2}bh\]
Now, on substituting the respective values we get,
\[\Rightarrow \dfrac{60\times 15}{2}\]
Now, on further simplification we get,
\[\Rightarrow 450\]sq. m
Now, the total area of the field is given by
\[\Rightarrow 1250+2500+1250+2100+700+450\]
Now, on further simplification we get,
\[\Rightarrow 8250\]sq. m
Hence, the correct option is (d).

Note:
Instead of considering the triangles (5), (6) and the rectangle (4) we can consider the whole bigger triangle and then find its area which will be the sum of those three areas. Both the methods give the same result but this reduces the number of steps.
It is important to note that the base of triangle (6) and the length of rectangle (4) will be the same which is the sum of 10 and 50 and it is also to be noted that while finding the height of the triangle in (6) we need to subtract the breadth of rectangle (4) from the height of triangle (1).