Question

A lamp post has half of its length in the mud, $\dfrac{1}{3}^{rd}$ of its length in water and $3\dfrac{1}{3}$m above the water but in the mud. Find the total length of the post.
A. $20$m
B. $15$m
C. $25$m
D. $30$m

Answer 1

Hint: In this problem we need to calculate the height or length of the lamp post. So, we will assume it as $x$ meters. Now from the given data we can clearly observe that the post is in mud, water below the mud and free air or above the ground. From this data we will draw a rough diagram and mention all the given data according to the diagram. Now we will calculate the total height of the post from the conditions that may be obtained from the diagram.

Complete step by step answer:
Given that,
A lamp post has half of its length in the mud, $\dfrac{1}{3}^{rd}$ of its length in water and $3\dfrac{1}{3}$m above the water but in the mud. Let the height or length of the post be $x$ meters, then the diagram related to this condition is shown below

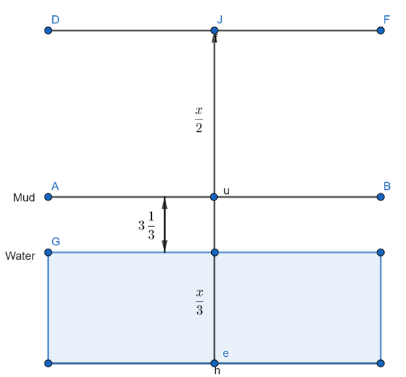
In the above figure, there are three levels, they are $AB$ is the mud level, $DF$ is the top level of the post and the water region or level is shaded with blue colour.
From the above diagram we can write that the length of the post below the mud level is the sum of the length of the pole which is in mud but not in water and the length of the pole which is water. Mathematically
$\begin{align}
  & 3\dfrac{1}{3}+\dfrac{x}{3}=\dfrac{x}{2} \\
 & \Rightarrow \dfrac{3\times 3+1}{3}+\dfrac{x}{3}=\dfrac{x}{2} \\
 & \Rightarrow \dfrac{10}{3}+\dfrac{x}{3}=\dfrac{x}{2} \\
 & \Rightarrow \dfrac{10+x}{3}=\dfrac{x}{2} \\
\end{align}$
Doing cross multiplication in the above equation, then we will get
$\begin{align}
  & \Rightarrow 2\left( 10+x \right)=3x \\
 & \Rightarrow 20+2x=3x \\
 & \Rightarrow 3x-2x=20 \\
 & \Rightarrow x=20 \\
\end{align}$
Hence the height or length of the post is $20$m.

So, the correct answer is “Option A”.

Note: For this the problem the diagrammatic representation gives the answer. In this problem they have asked to calculate the height or length of the post by giving the lengths of the required elements. Sometimes they may ask to calculate the length of post in the water by giving the value of total length and the remaining data which is given in the above problem. For this case also we will represent it in diagrammatic form then we will simply get an equation to calculate the required value.