Question

A lamp of luminous intensity $20\,Cd$ is hanging at a height of $40\,cm$ from the centre of a square table of side $60\,cm$ . The illuminance at the midpoint of the side of the table will be
A. $125$ lux
B. $100$ lux
C. $64$ lux
D. $32$ lux

Answer 1

Hint: Find the distance of the point where the illuminance of the lamp is to be calculated from the source of light (lamp). Using Lambert’s law, the illuminance can be calculated. Illuminance is the total luminous flux incident on a surface, per unit area.

Complete step by step answer:
We need to find the distance between the midpoint of the side of the table from the lamp. Let us draw an appropriate diagram for the same:

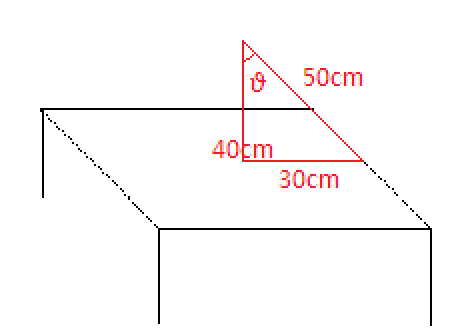
The height at which the lamp is hanging, $h = 40\,cm$ from the base of the table.
The length of the square table is $l = 60\,cm$ therefore, the base of the triangle will be half of the base length, as the lamp is placed exactly at the centre, $\dfrac{l}{2} = 30\,cm$
As we can clearly see, that $30,40$ forms a Pythagorean triplet with $50\,cm$ . Thus, the distance of the midpoint on the side from the lamp is $d = 50\,cm$
The given values are:
Luminous intensity of the lamp, $L = 20\,Cd$
$\cos \theta = \dfrac{4}{5}$ (from the diagram)
Lambert’s law states that light intensity lost during propagation is directly proportional to intensity and path length and inversely proportional to the square of distance from the source.
As per Lambert’s law, the illuminance at the midpoint of the side of the table will be given as:
$I = \dfrac{{L\cos \theta }}{{{d^2}}}$
Substituting the values, we get
$ \Rightarrow I = \dfrac{{20 \times \dfrac{4}{5}}}{{{{\left( {0.5} \right)}^2}}}$
$I = 64$ lux
The illuminance at the midpoint of the side of the table will be $64$ lux.

So, the correct answer is “Option C”.

Note:
Lambert’s law is used to find the loss of light intensity at a point.
The SI unit of illuminance is lux and the non-SI unit followed in the US is foot-candle.
Lambert’s law relates intensity with illuminance.
The illuminance is proportional to cosine of the angle between the distance and height.